题目内容
如图，点A、B在直线MN上，AB=14cm，⊙A、⊙B的半径均为1cm，⊙A以每秒2cm的速度自左向右运动，与此同时，⊙B的半径不断增大，其半径r（cm）与时间t（秒）之间的关系为r=1+t（t≥0），则当点出发后________秒两圆相切．
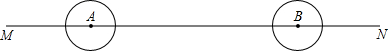
4或
或14或16
分析：根据两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
解答：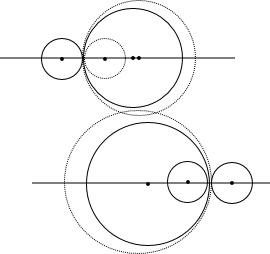
解：分四种情况考虑：
①当首次外切时，有2t+1+1+t=14，解得：t=4；
②当首次内切时，有2t+1+t-1=14，解得：t=；
③当再次内切时，有2t-（1+t-1）=14，解得：t=14；
④当再次外切时，有2t-（1+t）-1=14，解得：t=16．
所以当点A出发后4或或14或16秒两圆相切．
故答案为：4或或14或16．
点评：本题考查了两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
或14或16分析：根据两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
解答：
解：分四种情况考虑：①当首次外切时，有2t+1+1+t=14，解得：t=4；
②当首次内切时，有2t+1+t-1=14，解得：t=
；③当再次内切时，有2t-（1+t-1）=14，解得：t=14；
④当再次外切时，有2t-（1+t）-1=14，解得：t=16．
所以当点A出发后4或
或14或16秒两圆相切．故答案为：4或
或14或16．点评：本题考查了两圆相切时，两圆的半径与圆心距的关系，注意有4种情况．
练习册系列答案
相关题目
20、如图，点B、D 在直线MN上．已知∠1=∠2，请你再添上一个条件，使AB∥CD成立．并说明理由．
如图，点B，C分别在直线y=2x和直线y=kx上，A，D是x轴上两点，若四边形ABCD是长方形，且AB：AD=1：2，则k的值是（ ）