题目内容
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于A,B两点
与x轴交于A,B两点![]() 点A在点B左侧
点A在点B左侧![]() ,与y轴交于点
,与y轴交于点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上有一点P,使
在抛物线的对称轴上有一点P,使![]() 的值最小,求点P的坐标;
的值最小,求点P的坐标;
![]() 将抛物线在B,C之间的部分记为图象
将抛物线在B,C之间的部分记为图象![]() 包含B,C两点
包含B,C两点![]() ,若直线
,若直线![]() 与图象G有公共点,请直接写出b的取值范围.
与图象G有公共点,请直接写出b的取值范围.
【答案】(1)![]() .;(2)
.;(2)![]() ;(3)
;(3)![]()
【解析】
![]() 根据图象与y轴的交点,可得m的值,可得函数解析式;
根据图象与y轴的交点,可得m的值,可得函数解析式;
![]() 根据线段垂直平分线上的点到线段两端点的距离相等,可得M在对称轴上,根据两点之间线段最短,可得M点在线段AB上,根据自变量与函数值的对应关系,可得答案;
根据线段垂直平分线上的点到线段两端点的距离相等,可得M在对称轴上,根据两点之间线段最短,可得M点在线段AB上,根据自变量与函数值的对应关系,可得答案;
![]() 根据一次函数图象与区域抛物线的交点,可得不等式组,根据解不等式组,可得答案.
根据一次函数图象与区域抛物线的交点,可得不等式组,根据解不等式组,可得答案.
解:![]() 由题意可得,
由题意可得,![]() .
.
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
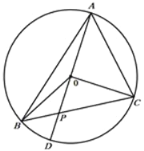
![]() 如图
如图
 ,
,
点A关于抛物线的对称轴对称的点是B,
连接BC交对称轴于点P,
则点P就是使得![]() 的值最小的点.
的值最小的点.
由![]() ,得对称轴是
,得对称轴是![]() ,
,
由![]() ,
,![]() ,得
,得
直线BC的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() .
.
![]() 当
当![]() 时,直线
时,直线![]() ,
,
解得![]() ;
;
直线![]() 与抛物线相切时,得
与抛物线相切时,得
![]() ,
,
![]() ,
,
解得![]() ,
,
符合题意的b的取值范围是![]() .
.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
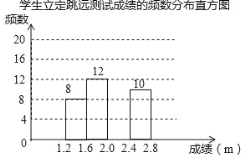
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有850名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?