题目内容
如图,∠ABC,∠ACB的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,连接AF,那么下列 结论正确的是
结论正确的是
①△BDF,△CEF都是等腰三角形;
②∠BFC=90°+ ∠BAC;
∠BAC;
③△ADE的周长为AB+AC;
④AF平分∠BAC.
- A.①③④
- B.①②
- C.①②③④
- D.②③④
C
分析:①根据平分线的性质、平行线的性质,借助于等量代换可求出∠DBF=∠DFB,即△BDF是等腰三角形,同理△CEF都是等腰三角形;
②利用两次三角形的内角和,以及平分线的性质,进行等量代换,可求的∠BFC和∠BAC之间的关系式;
③由①可得△ADE的周长为AB+AC;
④三角形的三条角平分线交于一点,可知AF平分∠BAC.
解答:①∵BF是∠ABC的角平分线,
∴∠ABF=∠CBF,
又∵DE∥BC,
∴∠CBF=∠DFB,
∴DB=DF即△BDF是等腰三角形,
同理∠ECF=∠EFC,
∴EF=EC,
∴△BDF,△CEF都是等腰三角形;
②在△ABC中,∠BAC+∠ABC+∠ACB=180°-----(1)
在△BFC中∠CFB+∠FBC+∠FCB=180°
即∠CFB+ ∠ABC+
∠ABC+ ∠ACB=180°----(2)
∠ACB=180°----(2)
(2)×2-(1)得②∠BFC=90°+ ∠BAC;
∠BAC;
③∵①△BDF,△CEF都是等腰三角形
∴BD=DF,EF=EC,
△ADE的周长=AD+DF+EF+AE=AD+BD+AE+EC=AB+AC;
④∵F是∠ABC,∠ACB的平分线的交点
∴第三条平分线必过其点,即AF平分∠BAC.
故选C.
点评:本题考查了等腰三角形的性质及角平分线的性质,以及三角形内角和定理解答,涉及面较广,需同学们仔细解答.
分析:①根据平分线的性质、平行线的性质,借助于等量代换可求出∠DBF=∠DFB,即△BDF是等腰三角形,同理△CEF都是等腰三角形;
②利用两次三角形的内角和,以及平分线的性质,进行等量代换,可求的∠BFC和∠BAC之间的关系式;
③由①可得△ADE的周长为AB+AC;
④三角形的三条角平分线交于一点,可知AF平分∠BAC.
解答:①∵BF是∠ABC的角平分线,
∴∠ABF=∠CBF,
又∵DE∥BC,
∴∠CBF=∠DFB,
∴DB=DF即△BDF是等腰三角形,
同理∠ECF=∠EFC,
∴EF=EC,
∴△BDF,△CEF都是等腰三角形;
②在△ABC中,∠BAC+∠ABC+∠ACB=180°-----(1)
在△BFC中∠CFB+∠FBC+∠FCB=180°
即∠CFB+
 ∠ABC+
∠ABC+ ∠ACB=180°----(2)
∠ACB=180°----(2)(2)×2-(1)得②∠BFC=90°+
 ∠BAC;
∠BAC;③∵①△BDF,△CEF都是等腰三角形
∴BD=DF,EF=EC,
△ADE的周长=AD+DF+EF+AE=AD+BD+AE+EC=AB+AC;
④∵F是∠ABC,∠ACB的平分线的交点
∴第三条平分线必过其点,即AF平分∠BAC.
故选C.
点评:本题考查了等腰三角形的性质及角平分线的性质,以及三角形内角和定理解答,涉及面较广,需同学们仔细解答.

练习册系列答案
相关题目
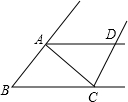 如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )
如图,△ABC的两个外角的平分线相交于D,若∠B=50°,则∠ADC=( )| A、60° | B、80° | C、65° | D、40° |
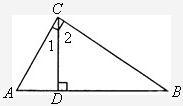
 ,且CB=CE.
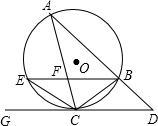
,且CB=CE. 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.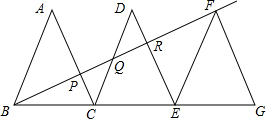 如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且
如图,△ABC、△DCE、△FEG是全等的三个等腰三角形,底边BC、CE、EG在同一直线上,且