题目内容
已知:二次函数的图象经过点A(1,0)和点B(2,1),且与y轴交点的纵坐标为m.
(1)若m为定值,求此二次函数的解析式;
(2)若二次函数的图象与x轴还有异于点A的另一个交点,求m的取值范围;
(3)若二次函数的图象截直线y=-x+1所得线段的长为 ,确定m的值.
,确定m的值.
解:(1)若m为定值,设二次函数解析式为y=ax2+bx+m,
把A(1,0)和B(2,1)代入上式,得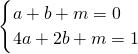 ,
,
解得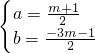 ,
,
则二次函数解析式为y= x2-
x2- x+m;
x+m;
(2)若二次函数的图象与x轴还有异于点A的另一个交点,
则 x2-
x2- x+m=0有两个不相等的实数根,
x+m=0有两个不相等的实数根,
故△>0,
即(- )2-4×
)2-4× m>0,
m>0,
整理得,m2-2m+1>0,
(m-1)2>0,
解得m≠1;
 ≠0,
≠0,
解得m≠-1;
则m的取值范围为m≠±1;
(3)设二次函数y= x2-
x2- x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2).
x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2).
令 x2-
x2- x+m=-x+1,
x+m=-x+1,
整理,得(m+1)x2--(3m-1)x+2m-2=0,
∴x1+x2=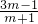 ,x1•x2=
,x1•x2=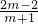 ;
;
∴(x1-x2)2=(x1+x2)2-4x1•x2=(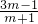 )2-4×
)2-4×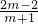 =(
=(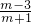 )2;
)2;
∵y=-x+1,
∴y1-y2=(-x1+1)-(-x2+1)=-(x1-x2),
∴(y1-y2)2=(x1-x2)2=(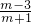 )2;
)2;
又∵MN=2 ,
,
∴(x1-x2)2+(y1-y2)2=(2 )2,
)2,
∴2(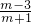 )2=8,
)2=8,
∴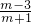 =±2,
=±2,
∴m1=-5,m2= .
.
故所求m的值为-5或 .
.
分析:(1)由于二次函数的图象与y轴交点的纵坐标为m,所以可设二次函数解析式为y=ax2+bx+m,把A(1,0)和B(2,1)代入,运用待定系数法即可求出此二次函数的解析式为y= x2-
x2- x+m;
x+m;
(2)由于二次函数为y= x2-
x2- x+m的图象与x轴有两个交点,所以一元二次方程
x+m的图象与x轴有两个交点,所以一元二次方程 x2-
x2- x+m=0的判别式△>0且
x+m=0的判别式△>0且 ≠0,由此可求出m的取值范围;
≠0,由此可求出m的取值范围;
(3)设二次函数y= x2-
x2- x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2),先由一元二次方程根与系数的关系求出(x1-x2)2=(x1+x2)2-4x1•x2=(
x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2),先由一元二次方程根与系数的关系求出(x1-x2)2=(x1+x2)2-4x1•x2=(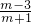 )2,再根据线段MN的长为2
)2,再根据线段MN的长为2 ,运用两点间的距离公式(x1-x2)2+(y1-y2)2=MN2,即可求出m的值.
,运用两点间的距离公式(x1-x2)2+(y1-y2)2=MN2,即可求出m的值.
点评:本题主要考查了运用待定系数法求二次函数的解析式,二次函数与一元二次方程的关系及两点间的距离公式,综合性较强,有一定难度.
把A(1,0)和B(2,1)代入上式,得
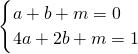 ,
,解得
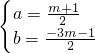 ,
,则二次函数解析式为y=
 x2-
x2- x+m;
x+m;(2)若二次函数的图象与x轴还有异于点A的另一个交点,
则
 x2-
x2- x+m=0有两个不相等的实数根,
x+m=0有两个不相等的实数根,故△>0,
即(-
 )2-4×
)2-4× m>0,
m>0,整理得,m2-2m+1>0,
(m-1)2>0,
解得m≠1;
 ≠0,
≠0,解得m≠-1;
则m的取值范围为m≠±1;
(3)设二次函数y=
 x2-
x2- x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2).
x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2).令
 x2-
x2- x+m=-x+1,
x+m=-x+1,整理,得(m+1)x2--(3m-1)x+2m-2=0,
∴x1+x2=
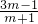 ,x1•x2=
,x1•x2=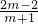 ;
;∴(x1-x2)2=(x1+x2)2-4x1•x2=(
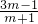 )2-4×
)2-4×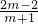 =(
=(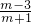 )2;
)2;∵y=-x+1,
∴y1-y2=(-x1+1)-(-x2+1)=-(x1-x2),
∴(y1-y2)2=(x1-x2)2=(
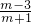 )2;
)2;又∵MN=2
 ,
,∴(x1-x2)2+(y1-y2)2=(2
 )2,
)2,∴2(
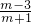 )2=8,
)2=8,∴
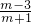 =±2,
=±2,∴m1=-5,m2=
 .
.故所求m的值为-5或
 .
.分析:(1)由于二次函数的图象与y轴交点的纵坐标为m,所以可设二次函数解析式为y=ax2+bx+m,把A(1,0)和B(2,1)代入,运用待定系数法即可求出此二次函数的解析式为y=
 x2-
x2- x+m;
x+m;(2)由于二次函数为y=
 x2-
x2- x+m的图象与x轴有两个交点,所以一元二次方程
x+m的图象与x轴有两个交点,所以一元二次方程 x2-
x2- x+m=0的判别式△>0且
x+m=0的判别式△>0且 ≠0,由此可求出m的取值范围;
≠0,由此可求出m的取值范围;(3)设二次函数y=
 x2-
x2- x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2),先由一元二次方程根与系数的关系求出(x1-x2)2=(x1+x2)2-4x1•x2=(
x+m的图象截直线y=-x+1所得线段为MN,且M(x1,y1),N(x2,y2),先由一元二次方程根与系数的关系求出(x1-x2)2=(x1+x2)2-4x1•x2=(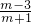 )2,再根据线段MN的长为2
)2,再根据线段MN的长为2 ,运用两点间的距离公式(x1-x2)2+(y1-y2)2=MN2,即可求出m的值.
,运用两点间的距离公式(x1-x2)2+(y1-y2)2=MN2,即可求出m的值.点评:本题主要考查了运用待定系数法求二次函数的解析式,二次函数与一元二次方程的关系及两点间的距离公式,综合性较强,有一定难度.

练习册系列答案
相关题目