题目内容
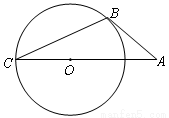
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C.若∠A=40,则∠C=_____
25°.
【解析】
试题分析:连接OB,AB与⊙O相切于点B,得到∠OBA=90°,根据三角形内角和得到∠AOB的度数,然后用三角形外角的性质求出∠C的度数.
试题解析:如图:连接OB,

∵AB与⊙O相切于点B,
∴∠OBA=90°,
∵∠A=40°,
∴∠AOB=50°,
∵OB=OC,
∴∠C=∠OBC,
∵∠AOB=∠C+∠OBC=2∠C,
∴∠C=25°.
考点:切线的性质;圆周角定理.

练习册系列答案
相关题目

 的结果是( )
的结果是( ) B.
B. C.
C. D.
D.
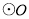 直径,
直径,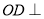 弦
弦 于点
于点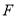 ,且交
,且交 于点
于点 ,若
,若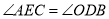 .
.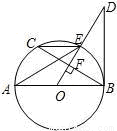
 和
和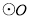 的位置关系,并给出证明;
的位置关系,并给出证明;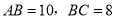 时,求
时,求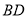 的长.
的长.

