题目内容
27、如图，OA，OB是⊙O的两条半径，BC是⊙O的切线，且∠AOB=84°，则∠ABC的度数为42
度．分析：先根据条件求得∠OBA=（180°-84°）÷2=48°，再根据BC是⊙O的切线，∠OBC=90°，求出∠ABC=42°．
解答：解：∵∠AOB=84°，OA=OB，
∴∠OBA=（180°-84°）÷2=48°；
∵BC是⊙O的切线，
∴∠OBC=90°，
∴∠ABC=∠OBC-∠OBA=42°．
∴∠OBA=（180°-84°）÷2=48°；
∵BC是⊙O的切线，
∴∠OBC=90°，
∴∠ABC=∠OBC-∠OBA=42°．
点评：本题用到的知识点为：圆心和切点的连线垂直于切线，等边对等角．
练习册系列答案
相关题目
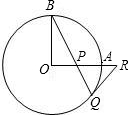如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的直线交OA延长线于点R，且RP=RQ
如图，OA、OB是两条互相垂直的半径，且OA=4，C为OB的中点，以OB为直径作半圆，CP∥OA，交
16、如图，OA和OB是⊙O的半径，并且OA⊥OB．P是OA上的任意一点，BP的延长线交⊙O于点Q，点R在OA的延长线上，且RP=RQ．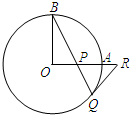
如图，OA和OB是⊙O的半径，OB=2，OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的⊙O的切线交OA延长线于点R．
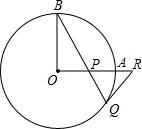如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的直线交OA延长线于点R，且RP=RQ