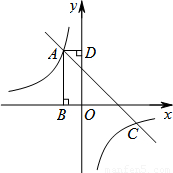
题目内容
如图,矩形ABOD的顶点A是函数y=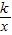 与函数y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,且矩形ABOD的面积为3.
与函数y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,且矩形ABOD的面积为3.(1)求两函数的解析式.
(2)求两函数的交点A、C的坐标.
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.
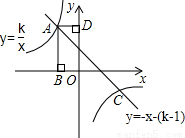
【答案】分析:(1)根据反比例函数系数k的几何意义和矩形ABOD的面积为3求出k的值;
(2)将两函数解析式组成方程组,求出其解,即得交点A、C的坐标;
(3)设直线y=-x+2与y轴的交点坐标为M(0,2),根据S△ABC=5,求出|PM|的值即可求出m的值.
解答:解:(1)设点A的坐标为(x,y),
∵点A在第二象限,
∴x<0,y>0,
∵S矩形ABOD=|AB|•|AD|=|x|•|y|=3,
∴-xy=3,
又∵y= ,
,
∴xy=k,
∴k=-3.
∴反比例函数的解析式为y=- ,一次函数的解析式为y=-x+2.
,一次函数的解析式为y=-x+2.
(2)由 ,
,
解得 ,
, .
.
∴点A、C的坐标分别为(-1,3),(3,-1).
(3)设点P的坐标为(0,m),
直线y=-x+2与y轴的交点坐标为M(0,2),
∵S△APC=S△AMP+S△CMP= |PM|(|x1|+|x2|)=5.
|PM|(|x1|+|x2|)=5.
∴|PM|= ,即|m-2|=
,即|m-2|= ,
,
∴m= 或m=-
或m=- ,
,
∴点P的坐标为(0, )或(0,-
)或(0,- ).
).
点评:此题考查了反比例函数的几何意义及函数图象交点和方程组的解关系,求出各交点坐标是解题的关键.
(2)将两函数解析式组成方程组,求出其解,即得交点A、C的坐标;
(3)设直线y=-x+2与y轴的交点坐标为M(0,2),根据S△ABC=5,求出|PM|的值即可求出m的值.
解答:解:(1)设点A的坐标为(x,y),
∵点A在第二象限,
∴x<0,y>0,
∵S矩形ABOD=|AB|•|AD|=|x|•|y|=3,
∴-xy=3,
又∵y=
 ,
,∴xy=k,
∴k=-3.
∴反比例函数的解析式为y=-
 ,一次函数的解析式为y=-x+2.
,一次函数的解析式为y=-x+2.(2)由
 ,
,解得
 ,
, .
.∴点A、C的坐标分别为(-1,3),(3,-1).
(3)设点P的坐标为(0,m),
直线y=-x+2与y轴的交点坐标为M(0,2),
∵S△APC=S△AMP+S△CMP=
 |PM|(|x1|+|x2|)=5.
|PM|(|x1|+|x2|)=5.
∴|PM|=
 ,即|m-2|=
,即|m-2|= ,
,∴m=
 或m=-
或m=- ,
,∴点P的坐标为(0,
 )或(0,-
)或(0,- ).
).点评:此题考查了反比例函数的几何意义及函数图象交点和方程组的解关系,求出各交点坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
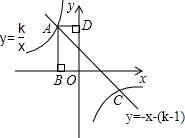 如图,矩形ABOD的顶点A是函数y=
如图,矩形ABOD的顶点A是函数y=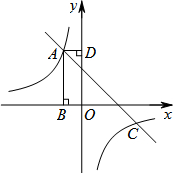 如图,矩形ABOD的顶点A是函数
如图,矩形ABOD的顶点A是函数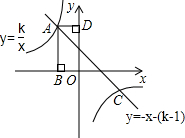 如图,矩形ABOD的顶点A是函数y=
如图,矩形ABOD的顶点A是函数y= 与函数y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,且矩形ABOD的面积为3.
与函数y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,AD⊥y轴于D,且矩形ABOD的面积为3.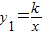 与函数y2=-x-(k+1)的图象在第二象限内的交点,AB⊥x轴于点B,AD⊥y轴于点D,且矩形ABOD的面积为3.
与函数y2=-x-(k+1)的图象在第二象限内的交点,AB⊥x轴于点B,AD⊥y轴于点D,且矩形ABOD的面积为3.