题目内容
 如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A,B两点,若OA:OB=3:1,求m的值.________.
如图,抛物线y=-x2+2(m+1)x+m+3与x轴交于A,B两点,若OA:OB=3:1,求m的值.________.
m=0
分析:先根据OA:OB=3:1设出A、B两点横坐标的未知数,再根据两根之和公式与两根之积公式解答即可.
解答:设B(-k,0),则A(3k,0).
∴-k,3k是方程-x2+2(m+1)x+m+3=0的两根,
∴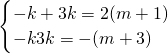 .
.
解得:m=0或- ,
,
∵都满足△>0,
如图:若x1,x2是方程-x2+2(m+1)x+m+3=0的两根,
则x1•x2=-(m+3)<0,x1+x2=2(m+1)>0,
当m=- 时,x1+x2=2(m+1)=-
时,x1+x2=2(m+1)=- <0,
<0,
∴m=- 不合题意,舍去.
不合题意,舍去.
∴m=0.
点评:抛物线与x轴相交,那么就要利用一元二次方程的两根之和公式与两根之积公式求解.
分析:先根据OA:OB=3:1设出A、B两点横坐标的未知数,再根据两根之和公式与两根之积公式解答即可.
解答:设B(-k,0),则A(3k,0).
∴-k,3k是方程-x2+2(m+1)x+m+3=0的两根,
∴
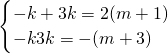 .
.解得:m=0或-
 ,
,∵都满足△>0,
如图:若x1,x2是方程-x2+2(m+1)x+m+3=0的两根,
则x1•x2=-(m+3)<0,x1+x2=2(m+1)>0,
当m=-
 时,x1+x2=2(m+1)=-
时,x1+x2=2(m+1)=- <0,
<0,∴m=-
 不合题意,舍去.
不合题意,舍去.∴m=0.
点评:抛物线与x轴相交,那么就要利用一元二次方程的两根之和公式与两根之积公式求解.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG| 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4). 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由. .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.