题目内容
如图,在?ABCD中,P1、P2、P3…Pn-1是BD的n等分点,连接AP2,并延长交BC于点E,连接APn-2并延长交CD于点F.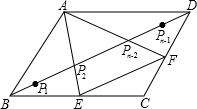 (1)求证:EF∥BD;
(1)求证:EF∥BD;(2)设?ABCD的面积是S,若S△AEF=
| 3 | 8 |
分析:①根据AD∥BC,AB∥DC,证明△Pn-2FD∽△Pn-2AB,△P2BE∽△P2DA,利用其相似比可得
=
,然后即可证明.
②由①可知
=
,同理可证S△ABE=
S,从而知S△ECF=
(
)2S,然后解
S=S-2×
S-
(
)2S,此方程即可.
| APn-2 |
| Pn-2F |
| AP2 |
| P2F |
②由①可知
| DF |
| AB |
| 2 |
| n-2 |
| 1 |
| n-2 |
| 1 |
| 2 |
| n-4 |
| n-2 |
| 3 |
| 8 |
| 1 |
| n-2 |
| 1 |
| 2 |
| n-4 |
| n-2 |
解答:(1)证明:∵AD∥BC,AB∥DC,
∴△Pn-2FD∽△Pn-2AB,△P2BE∽△P2DA
∴
=
=
,
=
=
即
=
,
∴EF∥BD.
(2)解:由①可知
=
,
∴S△AFD=
S,
同理可证S△ABE=
S
∴
=
,
∴
=
=1-
=
,
从而知S△ECF=
(
)2S,
已知S△AEF=
S,
∴
S=S-2×
S-
(
)2S,
即1-
-
=
解方程得n=6.
∴△Pn-2FD∽△Pn-2AB,△P2BE∽△P2DA
∴
| APn-2 |
| Pn-2F |
| BPn-2 |
| Pn-2D |
| n-2 |
| 2 |
| AP2 |
| P2E |
| DP2 |
| P2B |
| n-2 |
| 2 |
即
| APn-2 |
| Pn-2F |
| AP2 |
| P2E |
∴EF∥BD.
(2)解:由①可知
| DF |
| AB |
| 2 |
| n-2 |
∴S△AFD=
| 1 |
| n-2 |
同理可证S△ABE=
| 1 |
| n-2 |
∴
| DF |
| DC |
| 2 |
| n-2 |
∴
| FC |
| DC |
| DC-DF |
| DC |
| DF |
| DC |
| n-4 |
| n-2 |
从而知S△ECF=
| 1 |
| 2 |
| n-4 |
| n-2 |
已知S△AEF=
| 3 |
| 8 |
∴
| 3 |
| 8 |
| 1 |
| n-2 |
| 1 |
| 2 |
| n-4 |
| n-2 |
即1-
| 2 |
| n-2 |
| (n-4)2 |
| 2(n-2)2 |
| 3 |
| 8 |
解方程得n=6.
点评:此题主要考查学生对相似三角形的判定与性质和平行四边形的性质的理解和掌握,此题的难点是得出
S=S-2×
S-
(
)2S,此关系式,因此此题有一定难度,属于中档题.
| 3 |
| 8 |
| 1 |
| n-2 |
| 1 |
| 2 |
| n-4 |
| n-2 |

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=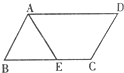 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.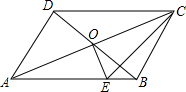 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是