Question

如图，已知反比例函数y=

k

x

(k＞0)的图象经过Rt△OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为4，则k=

 

．

Answer 1

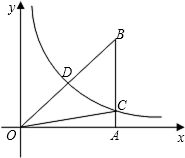
分析：过D点作x轴的垂线交x轴于E点，可得到四边形DBAE，和三角形OBC的面积相等，通过面积转化，可求出k的值．

解答：解：过D点作x轴的垂线交x轴于E点，
∵△ODE的面积和△OAC的面积相等．
∴△OBC的面积和四边形DEAB的面积相等且为4．
设D点的横坐标为x，纵坐标就为

k

x

，
∵D为OB的中点．
∴EA=x，AB=

2k

x

，
∴四边形DEAB的面积可表示为：

1

2

（

k

x

+

2k

x

）x=4
k=

8

3

．
故答案为：

8

3

．

点评：本题考查反比例函数的综合运用，关键是知道反比例函数图象上的点和坐标轴构成的三角形面积的特点以及根据面积转化求出k的值．