题目内容
 某星期天,小明和他的爸爸开着一辆满载西瓜的大卡车首次到某古城销售,来到城门下才发现古城门为抛物线形状(如图所示).小明的爸爸把车停在城门外,仔细端详城门的高和宽以及自己卡车的大小,十分担心卡车是否能够顺利通过.经询问得知,城门底部的宽为6米,最高点距离地面5米.如果卡车的高是4米,顶部宽是2.8米,那么卡车能否顺利通过?说明理由.(
某星期天,小明和他的爸爸开着一辆满载西瓜的大卡车首次到某古城销售,来到城门下才发现古城门为抛物线形状(如图所示).小明的爸爸把车停在城门外,仔细端详城门的高和宽以及自己卡车的大小,十分担心卡车是否能够顺利通过.经询问得知,城门底部的宽为6米,最高点距离地面5米.如果卡车的高是4米,顶部宽是2.8米,那么卡车能否顺利通过?说明理由.(| 5 |
分析:令抛物线y=ax2+5,再将B点坐标求出,设E点坐标为:(1.4,y),可求出抛物线上E点到地面的高度,进而得出答案.
解答:解:根据题意得出,设解析式为:y=ax2+5,
∵城门底部的宽为6米,最高点距离地面5米,
∴图象上点的B坐标为:(3,0),代入函数解析式得:
0=9a+5,
解得:a=-
,
∴解析式为:y=-
x2+5;
∵顶部宽是2.8米,
∴设E点坐标为:(1.4,y),
∴y=-
×1.42+5≈-1.1+5=3.9<4,
∴卡车不能顺利通过.
∵城门底部的宽为6米,最高点距离地面5米,
∴图象上点的B坐标为:(3,0),代入函数解析式得:
0=9a+5,
解得:a=-
| 5 |
| 9 |
∴解析式为:y=-
| 5 |
| 9 |
∵顶部宽是2.8米,
∴设E点坐标为:(1.4,y),
∴y=-
| 5 |
| 9 |
∴卡车不能顺利通过.
点评:此题主要考查了二次函数的应用,根据已知图象位置假设出正确的解析式是解题关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 某星期天,小明和他的爸爸开着一辆满载西瓜的大卡车首次到某古城销售,来到城门下才发现古城门为抛物线形状(如图所示).小明的爸爸把车停在城门外,仔细端详城门的高和宽以及自己卡车的大小,十分担心卡车是否能够顺利通过.经询问得知,城门底部的宽为6米,最高点距离地面5米.如果卡车的高是4米,顶部宽是2.8米,那么卡车能否顺利通过?说明理由.(
某星期天,小明和他的爸爸开着一辆满载西瓜的大卡车首次到某古城销售,来到城门下才发现古城门为抛物线形状(如图所示).小明的爸爸把车停在城门外,仔细端详城门的高和宽以及自己卡车的大小,十分担心卡车是否能够顺利通过.经询问得知,城门底部的宽为6米,最高点距离地面5米.如果卡车的高是4米,顶部宽是2.8米,那么卡车能否顺利通过?说明理由.(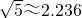 )
) )
)