题目内容
 如图,DE是△ABC的中位线,S△ADE=3,则S四边形DBCE=
如图,DE是△ABC的中位线,S△ADE=3,则S四边形DBCE=
- A.9
- B.12
- C.6
- D.8
A
分析:由DE是△ABC的中位线,根据三角形中位线的性质,可得DE∥BC,DE= BC,继而可证得△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,即可求得△ABC的面积,继而可求得四边形DBCE的面积.
BC,继而可证得△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,即可求得△ABC的面积,继而可求得四边形DBCE的面积.
解答:∵DE是△ABC的中位线,
∴DE∥BC,DE= BC,
BC,
∴△ADE∽△ABC,
∴ =(
=( )2=
)2= ,
,
∵S△ADE=3,
∴S△ABC=12,
∴S四边形DBCE=S△ABC-S△ADE=12-3=9.
故选A.
点评:此题考查了相似三角形的判定与性质与三角形中位线的性质.此题比较简单,解题的关键是注意相似三角形的面积比等于相似比的平方定理的应用,注意数形结合思想的应用.
分析:由DE是△ABC的中位线,根据三角形中位线的性质,可得DE∥BC,DE=
 BC,继而可证得△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,即可求得△ABC的面积,继而可求得四边形DBCE的面积.
BC,继而可证得△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,即可求得△ABC的面积,继而可求得四边形DBCE的面积.解答:∵DE是△ABC的中位线,
∴DE∥BC,DE=
 BC,
BC,∴△ADE∽△ABC,
∴
 =(
=( )2=
)2= ,
,∵S△ADE=3,
∴S△ABC=12,
∴S四边形DBCE=S△ABC-S△ADE=12-3=9.
故选A.
点评:此题考查了相似三角形的判定与性质与三角形中位线的性质.此题比较简单,解题的关键是注意相似三角形的面积比等于相似比的平方定理的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
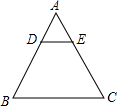 已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )
已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )| A、7.5 | B、15 | C、30 | D、24 |
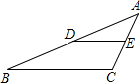 如图,DE是△ABC的中位线,则△ADE和四边形BCED的面积之比为( )
如图,DE是△ABC的中位线,则△ADE和四边形BCED的面积之比为( )| A、1:2 | B、1:3 | C、1:4 | D、以上都不对 |
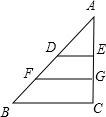 如图,DE是△ABC的中位线,FG是梯形BCED的中位线,若BC=16cm,则FG的长是( )
如图,DE是△ABC的中位线,FG是梯形BCED的中位线,若BC=16cm,则FG的长是( )| A、6 | B、8 | C、10 | D、12 |
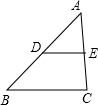 如图,DE是△ABC的中位线,若BC=6,则DE=
如图,DE是△ABC的中位线,若BC=6,则DE= 16、已知:如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=
16、已知:如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=