题目内容
试利用因式分解的方法说明两个连续奇数的平方差一定是8的倍数
答案:
解析:
解析:
|
解:设两个连续奇数分别为2n+1,2n+3 则(2n+3)2-(2n+1)2=(2n+3+2n+1)(2n+3-2n-1) =2(4n+4)=8(n+1) ∴(2n+3)2-(2n+1)2一定是8的倍数. 分析:两个连续奇数可表示为2n+1,2n+3,只需利用平方差公式将(2n+3)2-(2n+1)2分解因式后即可 |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
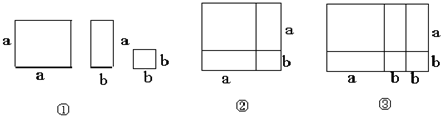
 利用十字相乘法把二次三项式分解因式的方法叫做十字相乘法,阅读用十字相乘法因式分解x2-5x+6.即:x2-5x+6=(x-2)(x-3)
利用十字相乘法把二次三项式分解因式的方法叫做十字相乘法,阅读用十字相乘法因式分解x2-5x+6.即:x2-5x+6=(x-2)(x-3)