题目内容
 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为 的中点,DE垂直于AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论一定错误的是
的中点,DE垂直于AC的延长线于E,连接BC,若DE=6cm,CE=2cm,下列结论一定错误的是
- A.DE是⊙O的切线
- B.直径AB长为20cm
- C.弦AC长为16cm
- D.C为
 的中点
的中点
D
分析:AB是圆的直径,则∠ACB=90°,根据DE垂直于AC的延长线于E,可以证得ED∥BC,则DE⊥OD,即可证得DE是圆的切线,根据切割线定理即可求得AC的长,连接OD,交BC与点F,则四边形DECF是矩形,根据垂径定理即可求得半径.
解答: 解:连接OD,OC.
解:连接OD,OC.
∵D是弧BC的中点,则OD⊥BC,
∴DE是圆的切线.故A正确;
∴DE2=CE•AE
即:36=2AE
∴AE=18,则AC=AE-CE=18-2=16cm.故C正确;
∵AB是圆的直径.
∴∠ACB=90°,
∵DE垂直于AC的延长线于E.
D是弧BC的中点,则OD⊥BC,
∴四边形CFDE是矩形.
∴CF=DE=6cm.BC=2CF=12cm.
在直角△ABC中,根据勾股定理可得:AB= =
=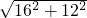 =20cm.故B正确;
=20cm.故B正确;
在直角△ABC中,AC=16,AB=20,
则∠ABC≠30°,
而D是弧BC的中点.
∴弧AC≠弧CD.
故D错误.
故选D.
点评:本题主要考查了垂径定理,以及切割线定理,利用垂径定理可以把圆的弦、半径的计算转化为解直角三角形.
分析:AB是圆的直径,则∠ACB=90°,根据DE垂直于AC的延长线于E,可以证得ED∥BC,则DE⊥OD,即可证得DE是圆的切线,根据切割线定理即可求得AC的长,连接OD,交BC与点F,则四边形DECF是矩形,根据垂径定理即可求得半径.
解答:
 解:连接OD,OC.
解:连接OD,OC.∵D是弧BC的中点,则OD⊥BC,
∴DE是圆的切线.故A正确;
∴DE2=CE•AE
即:36=2AE
∴AE=18,则AC=AE-CE=18-2=16cm.故C正确;
∵AB是圆的直径.
∴∠ACB=90°,
∵DE垂直于AC的延长线于E.
D是弧BC的中点,则OD⊥BC,
∴四边形CFDE是矩形.
∴CF=DE=6cm.BC=2CF=12cm.
在直角△ABC中,根据勾股定理可得:AB=
 =
=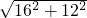 =20cm.故B正确;
=20cm.故B正确;在直角△ABC中,AC=16,AB=20,
则∠ABC≠30°,
而D是弧BC的中点.
∴弧AC≠弧CD.
故D错误.
故选D.
点评:本题主要考查了垂径定理,以及切割线定理,利用垂径定理可以把圆的弦、半径的计算转化为解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 16、如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E.
16、如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E.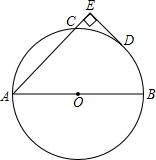 如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.
如图,已知AB、AC分别为⊙O的直径和弦,D为弧BC的中点,DE⊥AC于E,DE=6,AC=16.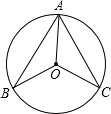 如图,已知AB、AC是⊙O的两条弦,且AB=AC,若∠BOC=100°,则∠BAO=
如图,已知AB、AC是⊙O的两条弦,且AB=AC,若∠BOC=100°,则∠BAO= (2008•宝山区二模)如图,已知AB、AC是⊙O的两条切线,切点分是点B、点C,∠BAC=60°,又⊙O的半径为2cm,则点A与点O的距离为
(2008•宝山区二模)如图,已知AB、AC是⊙O的两条切线,切点分是点B、点C,∠BAC=60°,又⊙O的半径为2cm,则点A与点O的距离为 如图,已知AB:AC=AD:AE,∠BAD=∠CAE.求证:∠ABC=∠ADE.
如图,已知AB:AC=AD:AE,∠BAD=∠CAE.求证:∠ABC=∠ADE.