Question

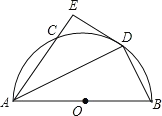
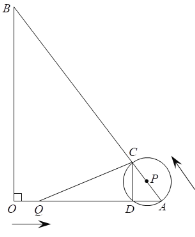
【题目】如图，在△AOB中，∠AOB＝90°，OA＝6，OB＝8，动点Q从点O出发，沿着OA方向以1个单位长度/秒的速度匀速运动，同时动点P从点A出发，沿着AB方向也以1个单位长度/秒的速度匀速运动，设运动时间为t秒（0＜t≤5），以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为C、D，连结CD、CQ．

⑴ 当点Q与点D重合时，求t的值；

⑵ 若△ACQ是等腰三角形，求t的值；

⑶ 若⊙P与线段QC只有一个公共点，求t的取值范围．

Answer 1

【答案】(1) ；(2) 或者或者．；(3) 或者

【解析】

(1)点Q与点D重合时，先证明 ,得到 ,利用平行线分线段成比例，找出AD的长，利用OQ+DA=OA,求出t的值．

(2)分三种情况进行讨论，AQ=AC；QC=CA；QC=QA，利用等腰三角形性质和三角形相似求出．

(3)一个交点，分情况讨论，当圆P与QC相切的时候，以及点Q与D重合的时候进行讨论，便可找出t的取值范围．

解： CA是直径，∠AOB＝90°．

．

在△AOB中，∠AOB＝90°，OA＝6，OB＝8中．

．

即 ．

当秒时，点Q与点D重合．

（2）若△ACQ是等腰三角形时，分三种情况讨论．

①当AQ=AC时，即AC=AQ=2t,OQ=t．

即：．

②当QC=CA时，即QC=CA=2t，由（1）知．

即： ．

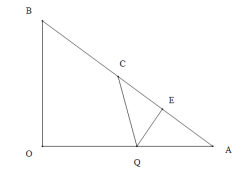
③当QC=QA时，过点Q作,则AE=t,AQ=6-t

∽．

．

即： ．

综上所述，当△ACQ是等腰三角形时，或者或者．

（3）当QC与圆P相切时， ．

．

．

∽

即： ．

解得：

当 时，圆P与QC只有一个交点．

当 时，由（1）知： ．

当 时，圆P与QC只有一个交点．

故：当圆P与QC只有 一个交点时，t的范围：或者．