题目内容
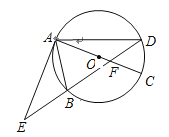
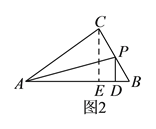
【题目】如图![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为
为![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 交折线
交折线![]() 于点
于点![]() ,设
,设![]() 的长为
的长为![]() ,
, ![]() 的面积为
的面积为![]() ,
, ![]() 关于
关于![]() 函数图象
函数图象![]() ,
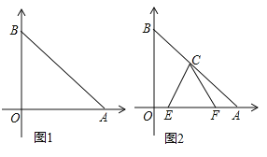
, ![]() 两段组成,如图
两段组成,如图![]() 所示.
所示.
(![]() )当
)当![]() 时,求
时,求![]() 的长.
的长.
(![]() )求图
)求图![]() 中的图象
中的图象![]() 段的函数解析式.
段的函数解析式.
(![]() )求
)求![]() 为何值时,
为何值时, ![]() 的面积为
的面积为![]() .
.


【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)由图2可知,当AD= ![]() 时,点P与点C重合,PD⊥AB于D可得∠PDA=90°,结合∠A=30°,可得AP=
时,点P与点C重合,PD⊥AB于D可得∠PDA=90°,结合∠A=30°,可得AP=![]() ,由此即可求出AP的长;
,由此即可求出AP的长;
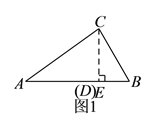
(2)由(1)可知,当AD= ![]() 时,点P与点C重合,此时AC=AP;如图1,过点C作CE⊥AB于点E,则AE=AD=4.5,由此在Rt△ACE中可求得CE的长,在Rt△BCE中可求得BE的长,从而可得AB的长;如图2,当点D在BE上时,易证△BDP∽△BEC,从而可得
时,点P与点C重合,此时AC=AP;如图1,过点C作CE⊥AB于点E,则AE=AD=4.5,由此在Rt△ACE中可求得CE的长,在Rt△BCE中可求得BE的长,从而可得AB的长;如图2,当点D在BE上时,易证△BDP∽△BEC,从而可得![]() ,结合BD=
,结合BD= ![]() 即可用含“
即可用含“![]() ”的式子表达出PD的长,从而由
”的式子表达出PD的长,从而由![]() AB·PD求得C2段的函数解析式;
AB·PD求得C2段的函数解析式;
(3)①当![]() 时,先由
时,先由![]() AD·PD求得C1段的函数解析式,再由
AD·PD求得C1段的函数解析式,再由![]() 列出方程求解即可得到对应的
列出方程求解即可得到对应的![]() 的值;②当
的值;②当![]() 时,由(2)中所得C2段的函数解析式中
时,由(2)中所得C2段的函数解析式中![]() 列出方程求解可得对应的
列出方程求解可得对应的![]() 的值;两者综合即可得到本问的解.
的值;两者综合即可得到本问的解.
试题解析:
(![]() )由图2可知,在
)由图2可知,在![]() ,当
,当 ![]() 时,点P与点C重合,
时,点P与点C重合,
∵∠ACB=90°,![]() ,
,
∴![]() .
.
(![]() )由图
)由图![]() 知,当
知,当![]() 时,
时, ![]() 最大,此时
最大,此时![]() 与
与![]() 重合,点D与点E重合,
重合,点D与点E重合,
∴![]() ,如图
,如图![]() ,过点
,过点![]() 作
作![]() ,
,
∴![]() ,
, ![]() ,
,
∵在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,在
,在![]() 中,
中, ![]() ,
,
如图![]() ,点
,点![]() 在线段
在线段![]() 上时,
上时,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ,
,
∴![]() ,
,
∴![]() .
.
(![]() )当
)当![]() 时,在
时,在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,当
,当![]() 时,
时, ![]() ,
,
由(![]() )知
)知![]() 时,
时, ![]() ,
, ![]() (舍)或
(舍)或![]() ,
,
即![]() 为
为![]() 或
或![]() 时,
时, ![]() 面积为
面积为![]() .
.

【题目】某商场购进一批LED灯泡与普通白炽灯炮,其进价与标价如下表,该商场购进LED灯泡与普通白炽灯炮共300个,LED灯泡按标价进行销售,而普通白炽灯炮按标价打九折销售,销售完这批灯泡后可以获利3200元。
(1)求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,并在不打折的情况下销售完,若销售完这批灯泡的获利不超过总进货价的28%,则最多购进LED灯泡多少个?
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |