题目内容
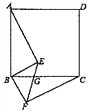
【题目】已知,直线![]() ,E为AB、CD间的一点,连接EA、EC.
,E为AB、CD间的一点,连接EA、EC.
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 如图
如图![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,
,![]() 与
与![]() 之间有何等量关系
之间有何等量关系![]() 并简要说明.
并简要说明.

【答案】(1)∠AEC=60°;(2)![]() ;(3)
;(3)![]() .
.
【解析】
分别过图1、图2和图3中的点E作直线EF∥AB,然后根据“平行线的判定和性质”结合各小题中的已知条件进行分析解答即可.
(1)如下图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1=∠A=20°,∠2=∠C=40°,
∴∠AEC=∠1+∠2=60°;

(2)如上图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠A=180°,∠2+∠C=180°,
∵∠A=x°,∠B=∠y°,
∴∠1=180°-x°,∠2=180°-y°,
∴∠AEC=∠1+∠2=360°-x°-y°;
(3)如上图3,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠A=180°,∠2=∠C,
∵∠A=![]() ,∠C=
,∠C=![]() ,
,
∴∠1=180°-![]() ,∠2=
,∠2=![]() ,
,
∴∠AEC=∠1+∠2=180°-![]() +
+![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目