题目内容
【题目】已知关于x的一元二次方程mx2﹣(m﹣1)x﹣1=0.
(1)求证:这个一元二次方程总有两个实数根;
(2)若二次函数y=mx2﹣(m﹣1)x﹣1有最大值0,则m的值为 ;
(3)若x1、x2是原方程的两根,且![]() =2x1x2+1,求m的值.
=2x1x2+1,求m的值.
【答案】(1)证明见解析;(2)-1;(3)m=![]() 或m=
或m=![]() .
.
【解析】
(1)先计算判别式得到△=(m+1)2,根据非负数的性质即可得到△≥0,于是利用判别式的意义即可得到结论;
(2)根据二次函数的性质得m<0且![]() =0,然后解方程即可;
=0,然后解方程即可;
(3)先根据根与系数的关系得到x1+x2=![]() ,x1x2=﹣
,x1x2=﹣![]() ,再把
,再把![]() =2x1x2+1变形得到
=2x1x2+1变形得到![]() =2x1x2+1,则
=2x1x2+1,则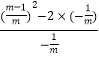 =2(﹣
=2(﹣![]() )+1,然后解关于m的方程即可.
)+1,然后解关于m的方程即可.
(1)证明:m≠0,
△=(m﹣1)2﹣4m×(﹣1)
=(m+1)2,
∵(m+1)2≥0,即△≥0,
∴这个一元二次方程总有两个实数根;
(2)解:∵二次函数y=mx2﹣(m﹣1)x﹣1有最大值0,
∴m<0且![]() =0,
=0,
∴m=﹣1;
故答案为﹣1.
(3)解:x1+x2=![]() ,x1x2=﹣
,x1x2=﹣![]() ,
,
∵![]() =2x1x2+1,
=2x1x2+1,
∴![]() =2x1x2+1,
=2x1x2+1,
∴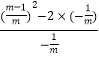 =2(﹣
=2(﹣![]() )+1,
)+1,
整理得m2+m﹣1=0,
∴m=![]() 或m=
或m=![]() .
.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目