Question

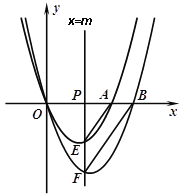
【题目】如图，动直线（）分别交x轴，抛物线和于点P，E，F，设点A，B为抛物线， 与x轴的一个交点，连结AE，BF．

（1）求点A，B的坐标.

(2）当时，判断直线AE与BF的位置关系，并说明理由.

（3）连结BE，当时，求△BEF的面积.

Answer 1

【答案】(1) 点A的坐标为（3，0），点B的坐标为（4，0）;（2）AE∥BF．（3）（Ⅰ）2；（Ⅱ） .

【解析】试题分析：（1）把y=0分别代入y=x2-3x和y=x2-4x中，进而得出A，B点坐标；

（2）利用锐角三角函数关系得出∠PAE=∠PBF，进而得出直线AE与BF的位置关系；

（3）利用AE∥BF，得出△PAE∽△PBF，进而求出m的值，即可得出△BEF的面积．

试题解析：（1）把y=0分别代入和中，

得： ，

解得x=0或x=3；

，

解得x=0或x=4

∴点A的坐标为（3，0），点B的坐标为（4，0）；

（2）直线AE与BF的位置关系是AE∥BF．

理由如下：

由题意得，点E的坐标为（m， ），

点F的坐标为（m， ）．

∴tan∠PAE= ，

∴tan∠PBF= ,

∴∠PAE=∠PBF，∴AE∥BF；

（3）（Ⅰ）如图1，

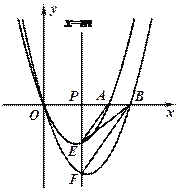
∵AE∥BF，∴△PAE∽△PBF，

∴，即，解得m=2．

∴；

（Ⅱ）如图2，

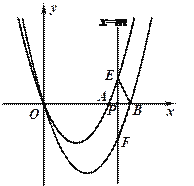
∵AE∥BF，∴△PAE∽△PBF，

∴，即，解得m=．

∴S△BEF=EFPB=××=．