题目内容
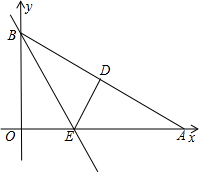
 如图,△AOB为正三角形,点B的坐标为(2,0),过点C(-2,0)作直线l交AO于D,交AB于E,且使△ADE和△DCO的面积相等,则直线l的解析式为
如图,△AOB为正三角形,点B的坐标为(2,0),过点C(-2,0)作直线l交AO于D,交AB于E,且使△ADE和△DCO的面积相等,则直线l的解析式为y=
x+
| ||
| 7 |
2
| ||
| 7 |
y=
x+
.
| ||
| 7 |
2
| ||
| 7 |
分析:根据S△DCO=S△ADE可知S△DCO+S四边形DOBE=S△ADE+S四边形DOBE,从而得到S△BCE=S△AOB,
根据△AOB为正三角形求出三角形的高,从而求出A点坐标,根据待定系数法求出AB的解析式,根据S△BCE=S△AOB,求出A点纵坐标,代入直线AB,可得E点横坐标,再利用待定系数法求出CD的解析式.
根据△AOB为正三角形求出三角形的高,从而求出A点坐标,根据待定系数法求出AB的解析式,根据S△BCE=S△AOB,求出A点纵坐标,代入直线AB,可得E点横坐标,再利用待定系数法求出CD的解析式.
解答:解:∵S△DCO=S△ADE,
∴S△DCO+S四边形DOBE=S△ADE+S四边形DOBE,
∴S△BCE=S△AOB,
∵△AOB为正三角形,B坐标为(2,0)知其边长为2,高为
,
∴点A(1,
).
∴S△AOB=
×2×
=
.
设E(x0,y0),则S△CBE=
×4×y0=2y0,
∵2y0=
,
∴y0=
,
由点A(1,
),B(2,0)得直线AB解析式为y=-
(x-2),
而E在直线AB上,则y0=-
(x0-2),
可得,x0=
,
∴点E(
,
),
又∵点C(-2,0),
∴解方程组
,
解得
,
∴直线L的解析式为:y=
x+
.
故答案为:y=
x+
.
∴S△DCO+S四边形DOBE=S△ADE+S四边形DOBE,
∴S△BCE=S△AOB,
∵△AOB为正三角形,B坐标为(2,0)知其边长为2,高为
| 3 |
∴点A(1,
| 3 |
∴S△AOB=
| 1 |
| 2 |
| 3 |
| 3 |
设E(x0,y0),则S△CBE=
| 1 |
| 2 |
∵2y0=
| 3 |
∴y0=
| ||
| 2 |
由点A(1,
| 3 |
| 3 |
而E在直线AB上,则y0=-
| 3 |
可得,x0=
| 3 |
| 2 |
∴点E(
| 3 |
| 2 |
| ||
| 2 |
又∵点C(-2,0),
∴解方程组
|
解得
|
∴直线L的解析式为:y=
| ||
| 7 |
2
| ||
| 7 |
故答案为:y=
| ||
| 7 |
2
| ||
| 7 |
点评:本题考查了一次函数综合题,涉及等积变换、待定系数法求函数解析式、等边三角形的性质等内容,是一道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 痕为BE.
痕为BE. 如图,A、B两点的坐标分别为(-3,0)、(0,3),C点在x轴的正半轴上,且到原点的距离为1.点P、Q分别从A、B两点同时出发,以相同的速度分别向x轴、y轴的正方向作匀速直线运动,直线PQ交直线AB于D.
如图,A、B两点的坐标分别为(-3,0)、(0,3),C点在x轴的正半轴上,且到原点的距离为1.点P、Q分别从A、B两点同时出发,以相同的速度分别向x轴、y轴的正方向作匀速直线运动,直线PQ交直线AB于D.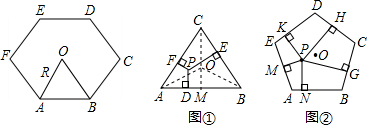 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?