题目内容
如图所示，已知⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若AD=3，AC=2，则cosD的值为
- A.
- B.
- C.
- D.
B
分析：根据圆周角定理的推论，得∠B=∠D．根据直径所对的圆周角是直角，得∠ACD=90°．
在直角三角形ACD中，根据勾股定理，得CD=
，则cosD=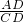
=．
解答：∵AD是⊙O的直径，
∴∠ACD=90°．
∵AD=3，AC=2，
∴CD=．
∴cosD==．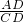
故选B．
点评：此题综合运用了圆周角定理的推论以及锐角三角函数的定义．
分析：根据圆周角定理的推论，得∠B=∠D．根据直径所对的圆周角是直角，得∠ACD=90°．
在直角三角形ACD中，根据勾股定理，得CD=
，则cosD=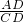=．解答：∵AD是⊙O的直径，
∴∠ACD=90°．
∵AD=3，AC=2，
∴CD=
．∴cosD=
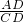=．故选B．
点评：此题综合运用了圆周角定理的推论以及锐角三角函数的定义．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
22、如图所示，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1m/s，点Q运动的速度是2m/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t s，解答下列问题：
19、如图所示，已知O是四边形ABCD内一点，OB=OC=OD，∠BCD=∠BAD=75°，则∠ADO+∠ABO=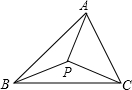
如图所示，已知P是△ABC内一点，试说明PA+PB+PC＞
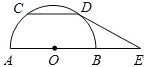如图所示，已知AB是半圆O的直径，弦CD∥AB，AB=10，CD=6，E是AB延长线上一点，BE=
20、如图所示，已知AB是半圆O的直径，∠BAC=22°，则∠B=