题目内容
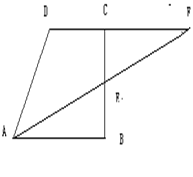
如图,正方形ABCD,E为AB上的动点,(E不与A、B重合)联结DE,作DE的中垂线,交AD于点F.
(1)若E为AB中点,则 .
.
(2)若E为AB的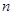 等分点(靠近点A),
等分点(靠近点A),
则 .
.
(1)若E为AB中点,则
 .
.(2)若E为AB的
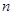 等分点(靠近点A),
等分点(靠近点A),则
 .
.
解:(1)设正方形ABCD的边长为m,由已知得:
AD=m,AE= m,
m,
由直角三角形DAE,根据勾股定理得:
DE= m,
m,
已知作DE的中垂线,交AD于点F,
∴DG= DE=
DE= m,
m,
由已知得:直角三角形DAE∽直角三角形DGF,
∴ ,
,
∴DF= m,
m,
∴ ,
,
故答案为: .
.
(2)由已知.若正方形ABCD的边长为1,则AE=
根据勾股定理得:DE= ,
,
DG= ,
,
由(1)直角三角形DAE∽直角三角形DGF,
得:DF= ,
,
∴
 ,
,
故答案为: .
.
AD=m,AE=
 m,
m,由直角三角形DAE,根据勾股定理得:
DE=
 m,
m,已知作DE的中垂线,交AD于点F,
∴DG=
 DE=
DE= m,
m,由已知得:直角三角形DAE∽直角三角形DGF,
∴
 ,
,∴DF=
 m,
m,∴
 ,
,故答案为:
 .
.(2)由已知.若正方形ABCD的边长为1,则AE=

根据勾股定理得:DE=
 ,
,DG=
 ,
,由(1)直角三角形DAE∽直角三角形DGF,
得:DF=
 ,
,∴

 ,
,故答案为:
 .
.
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
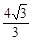 cm2 B.
cm2 B.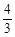 cm2 C.
cm2 C.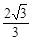 cm2 D.
cm2 D.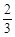 cm2
cm2 ,
, ,那么向量
,那么向量 ____________(结果用
____________(结果用 、
、 表示).
表示).

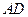 ∥
∥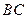 ,
,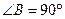 ,
,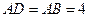 ,
,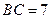 ,点E在BC边上,将△CDE沿DE折叠,点C恰好落在AB边上的点
,点E在BC边上,将△CDE沿DE折叠,点C恰好落在AB边上的点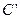 处.
处.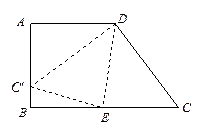
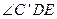 的度数;
的度数;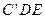 的面积.
的面积.



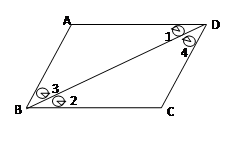
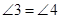 .
.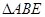 ≌
≌