题目内容
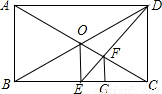
（2001•山东）如图所示，在矩形ABCD中，AC、BD相交于点O，OE⊥BC于E，连接DE交OC于点F，作FG⊥BC于G．（1）说明点G是线段BC的一个三等分点；
（2）请你依照上面的画法，在原图上画出BC的一个四等分点（保留作图痕迹，不必证明）．
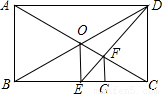
【答案】分析：（1）根据矩形对角线的性质可以判断E为BC的二等分点，再由OE∥CD，OE=
CD，得出EG=
GC，从而得出GC=
CE=
BC．
（2）依题意，根据平行线分线段成比例定理直接在图中作图即可．
解答：
解：（1）∵OE⊥BC，FG⊥BC，
∴OE∥CD．
∴
．
∵四边形ABCD是矩形，
∴AD∥BC．
∴
．
∴G是BC的三等分点；
（2）依题意画图如右．
点评：本题考查平行线分线段成比例定理，需要根据平行找准对应关系，要和相似三角形对应边成比例加以区别．
CD，得出EG=GC，从而得出GC=CE=BC．（2）依题意，根据平行线分线段成比例定理直接在图中作图即可．
解答：
解：（1）∵OE⊥BC，FG⊥BC，∴OE∥CD．
∴
．∵四边形ABCD是矩形，
∴AD∥BC．
∴
．∴G是BC的三等分点；
（2）依题意画图如右．
点评：本题考查平行线分线段成比例定理，需要根据平行找准对应关系，要和相似三角形对应边成比例加以区别．
练习册系列答案
名校课堂系列答案
相关题目
