题目内容
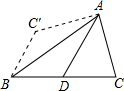 如图,AD是△ABC的中线,∠ADC=60°,把△ADC沿直线AD折过来,点C落在C′位置,如图BC=4,则BC′=________.
如图,AD是△ABC的中线,∠ADC=60°,把△ADC沿直线AD折过来,点C落在C′位置,如图BC=4,则BC′=________.
2
分析:根据等腰三角形的性质解答.
解答: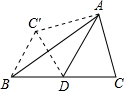 解:连接DC′,依题意有:DC′=DC,∠ADC′=∠ADC=60°,
解:连接DC′,依题意有:DC′=DC,∠ADC′=∠ADC=60°,
又∵BD=DC= BC=2,
BC=2,
∴∠BDC′+∠ADC′+∠ADC=180°.
∴DC′=BD=2,∠BDC′=60°.
∴∠DBC′=∠DC′B= (180°-∠BDC′)=60°.
(180°-∠BDC′)=60°.
∴△BDC′为等边三角形.
即:BC′=BD=DC′=2.
点评:解答此题时要注意对折以后的三角形与原三角形全等,再根据三角形内角和定理解答.
分析:根据等腰三角形的性质解答.
解答:
 解:连接DC′,依题意有:DC′=DC,∠ADC′=∠ADC=60°,
解:连接DC′,依题意有:DC′=DC,∠ADC′=∠ADC=60°,又∵BD=DC=
 BC=2,
BC=2,∴∠BDC′+∠ADC′+∠ADC=180°.
∴DC′=BD=2,∠BDC′=60°.
∴∠DBC′=∠DC′B=
 (180°-∠BDC′)=60°.
(180°-∠BDC′)=60°.∴△BDC′为等边三角形.
即:BC′=BD=DC′=2.
点评:解答此题时要注意对折以后的三角形与原三角形全等,再根据三角形内角和定理解答.

练习册系列答案
相关题目

 如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是
如图,AD是△ABC是角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的位置关系是 16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为
16、已知:如图,AD是△ABC的角平分线,且 AB:AC=3:2,则△ABD与△ACD的面积之比为 如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.
如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )
如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,如果△DEF的面积是2,那么△ABC的面积为( )