题目内容
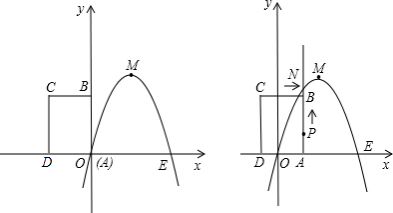
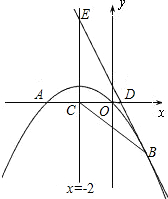
如图，已知抛物线经过点B(-2,3)、原点O和x轴上另一点A,它的对称轴与x轴交于点C（2，0），
1.求此抛物线的函数关系式；
2.联结CB, 在抛物线的对称轴上找一点E,使得CB=CE,求点E的坐标；
3.在(2)的条件下, 联结BE,设BE的中点为G,在抛物线的对称轴上是否存在点P，使得△PBG的周长最小？若存在，求出P点坐标；若不存在，请说明理由.
1.抛物线的解析式为：
2.
，
3.存在.
①当时，
，设点B关于直线x=2的对称点为D，其坐标为（6，3） 直线
的解析式为：
，∴
（2，
） ②当时，
,直线
的解析式为：
∴
（2，
） 综合①、②存在这样的点P，使得△PBG的周长最小，且点P的坐标为（2，）或（2，）
解析:略
练习册系列答案
相关题目
2x+1经过抛物线上一点B（2，m），且与y轴．直线x=-2分别交于点D、E．
（2013•衡阳）如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是x=-1．
如图，已知抛物线经过原点O和x轴上另一点A，它的对称轴x=2与x轴交于点C，直线y=-2x-1经过抛物线上一点B（-2，m），且与y轴、直线x=2分别交于点D、E，
如图，已知抛物线经过坐标原点，与x轴的另一个交点为A，且顶点M坐标为（1，2），