题目内容
如图,边长为1的等边△OAB,顶点A在x轴上,将△OAB绕点O顺时针旋转30°,使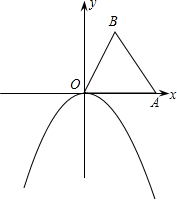 点A落在抛物线y=ax2(a<0)的图象上.
点A落在抛物线y=ax2(a<0)的图象上.(1)求抛物线y=ax2的表达式;
(2)等边△OAB继续绕点O顺时针旋转,使点A再次落在抛物线y=ax2的图象上.写出这个点的坐标和最少旋转的度数.
分析:(1)旋转角为30°是特殊角,此时OA1=OA=1,过A1作x轴的垂线,解直角三角形可得A1的坐标,再代入抛物线y=ax2可求解析式;
(2)根据抛物线的对称性,可猜想等边△OAB继续绕点O顺时针旋转,使点A再次落在抛物线y=ax2的图象上时,OA与x轴负半轴夹角为30°,再次旋转120°,此时点A与A1关于y轴对称.
(2)根据抛物线的对称性,可猜想等边△OAB继续绕点O顺时针旋转,使点A再次落在抛物线y=ax2的图象上时,OA与x轴负半轴夹角为30°,再次旋转120°,此时点A与A1关于y轴对称.
解答:解:(1)∵△OAB绕点O顺时针旋转30°,A(1,0),则A1(
,-
),
把x=
,y=-
代入y=ax2
得a=-
,
∴y=-
x2.
(2)等边△OAB继续绕点O顺时针旋转,使点A再次落在抛物线y=ax2的图象,这时旋转后点A坐标为A2(-
,-
),
旋转角为∠A2OA1=120°.
| ||
| 2 |
| 1 |
| 2 |
把x=
| ||
| 2 |
| 1 |
| 2 |
得a=-
| 2 |
| 3 |
∴y=-
| 2 |
| 3 |
(2)等边△OAB继续绕点O顺时针旋转,使点A再次落在抛物线y=ax2的图象,这时旋转后点A坐标为A2(-
| ||
| 2 |
| 1 |
| 2 |
旋转角为∠A2OA1=120°.
点评:本题考查了坐标系里的旋转问题,抛物线的对称性问题,充分体现了形数结合的数学思想.

练习册系列答案
相关题目
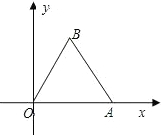 如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线
如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线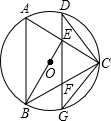 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
 (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长. (2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是
(2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是