题目内容
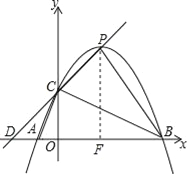
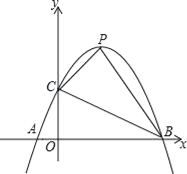
【题目】已知,如图,抛物线y=﹣x2+ax+b与x轴从左至右交于A、B两点,与y轴正半轴交于点C.设∠OCB=α,∠OCA=β,且tanα﹣tanβ=2,OC2=OAOB.
(1)△ABC是否为直角三角形?若是,请给出证明;若不是,请说明理由;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
【答案】(1)△ABC是直角三角形,理由见解析;(2)抛物线的解析式为:y=﹣x2+2x+1;(3)四边形ABPC的面积为![]() .
.
【解析】试题分析:(1)利用已知得出Rt△BOC∽Rt△COA,进而得出∠OCA+∠OCB=90°,即可得出答案;
(2)由题意可得,方程﹣x2+ax+b=0有两个不同的实数根,进而得出C点坐标,可得出b的值,再利用tanα=![]() ,tanβ=
,tanβ=![]() ,由tanα﹣tanβ=2,得出a的值进而得出答案;
,由tanα﹣tanβ=2,得出a的值进而得出答案;
(3)作PF⊥x轴于点F,根据S四边形ABPC=S△PDB﹣S△CDA=![]() DBPF﹣
DBPF﹣![]() DAOC,进而得出答案.
DAOC,进而得出答案.
试题解析:(1)△ABC是直角三角形.
理由如下:
∵OC2=OAOB,∴![]() =
=![]() ,
,
又∵∠BOC=∠COA=90°,∴Rt△BOC∽Rt△COA,∴∠OCB=∠OAC,
又∵∠OCA+∠OAC=90°,∴∠OCA+∠OCB=90°,
即∠ACB=90°,∴△ABC是直角三角形;
(2)∵抛物线与x轴交于A、B两点,
∴方程﹣x2+ax+b=0有两个不同的实数根,
设这两个根分别为x1、x2,且x1<x2,显然,x1<0,x2>0,
得A、B两点的坐标分别为A(x1,0)、B(x2,0),
由根与系数的关系,有x1+x2=a,x1x2=﹣b,
对于抛物线y=﹣x2+ax+b,当x=0时,y=b,∴C点的坐标为C(0,b);
由已知条件OC2=OAOB,得b2=(﹣x1)x2,即b2=﹣x1x2,∴b2=b,
∵点C在y轴的正半轴上,∴b>0,从而得b=1,
∵tanα=![]() ,tanβ=
,tanβ=![]() ,由tanα﹣tanβ=2,得
,由tanα﹣tanβ=2,得![]() ﹣
﹣![]() =2,即OB﹣OA=2OC,
=2,即OB﹣OA=2OC,
得x2﹣(﹣x1)=2b,x2+x1=2b,即a=2b,∴a=2,
∴抛物线的解析式为:y=﹣x2+2x+1;
(3)由抛物线的解析式y=﹣x2+2x+1,配方得:y=﹣(x﹣1)2+2,
∴其顶点P的坐标为P(1,2).
解方程﹣x2+2x+1=0,得x1=1﹣![]() ,x2=1+
,x2=1+![]() ,∴A(1﹣
,∴A(1﹣![]() ,0),B(1+
,0),B(1+![]() ,0),
,0),
解法一:设过P、C两点的直线与x轴交于点D,
直线的解析式为:y=kx+1,把P(1,2)坐标代入,得k=1,
∴直线PC:y=x+1,当y=0时,x=﹣1,即点D的坐标为D(﹣1,0).
∵﹣1<1﹣![]() ,∴点D在点A的左边,
,∴点D在点A的左边,
作PF⊥x轴于点F,
∴S四边形ABPC=S△PDB﹣S△CDA=![]() DBPF﹣
DBPF﹣![]() DAOC
DAOC
=![]() [(1+
[(1+![]() )+1]×2﹣
)+1]×2﹣![]() [(1﹣
[(1﹣![]() )+1]×1
)+1]×1
=![]() ,
,
即四边形ABPC的面积为![]() .
.
解法二:过点P作PF⊥x轴于点F,
则∴S四边形ABPC=S△OAC+S梯形COFP+S△PFB
=![]() OAOC+
OAOC+![]() (OC+PF)OF+
(OC+PF)OF+![]() FBPF
FBPF
=![]() (
(![]() ﹣1)×1+
﹣1)×1+![]() (1+2)×1+
(1+2)×1+![]() (1+
(1+![]() ﹣1)×2
﹣1)×2
=![]() ;
;
即四边形ABPC的面积为![]() .
.