题目内容
已知:A、B、C是⊙O上的三点,∠BAC是锐角,连接OB、OC,求证:∠BAC= ∠BOC.
∠BOC.
 解:如图所示:(1)圆心在圆周角一边上.
解:如图所示:(1)圆心在圆周角一边上.∵OA=OC,
∴∠A=∠C,
又∵∠BOC=∠A+∠C,
∴∠BAc=
 ∠BOC.
∠BOC.(2)由(1)可得,∠BAD=
 ∠BOD,∠CAD=
∠BOD,∠CAD= ∠COD,
∠COD,所以∠BAD+∠CAD=
 ∠BOD+
∠BOD+ ∠COD=
∠COD= (∠BOD+∠COD)=
(∠BOD+∠COD)= ∠BOC,
∠BOC,即∠BAC=
 ∠BOC.
∠BOC.(3)由(1)可得,∠BAD=
 ∠BOD,∠CAD=
∠BOD,∠CAD= ∠COD,
∠COD,所以∠CAD-∠BAD=
 ∠COD-
∠COD- ∠BOD=
∠BOD= (∠COD-∠BOD)=
(∠COD-∠BOD)= ∠BOC.
∠BOC.即∠BAC=
 ∠BOC.
∠BOC.分析:根据题意画出三种图形解答:(1)圆心在圆周角一边上,利用等腰三角形的性质;
(2)圆心在圆周角内部,利用(1)的结论;
(3)圆心在圆周角外部,利用(1)的结论.
点评:本题考查了圆周角定理,解答此题的关键是分类讨论,并且会利用求出的结论解答后面的问题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
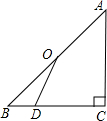 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.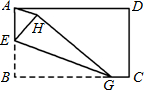 12、如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为
12、如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为