题目内容
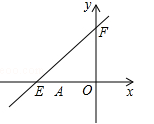
(10分)如图,直线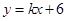 与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
与x轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点, 当点P运动过程中,试写出三角形OPA的面积s与x的函数关系式,并写出自变量x的取值范围;
当点P运动过程中,试写出三角形OPA的面积s与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为 ,并说明理由.
,并说明理由.
(1)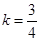 ;(2)
;(2)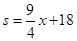 (-8<
(-8< <0);(3)P(
<0);(3)P(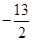 ,
,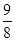 ).
).
解析试题分析:(1)将点E坐标(﹣8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(﹣6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为 代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
试题解析:(1)∵点E(﹣8,0)在直线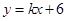 上,∴
上,∴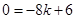 ,∴
,∴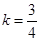 ;
;
(2)∵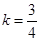 ,∴直线的解析式为:
,∴直线的解析式为: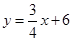 ,∵P点在
,∵P点在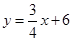 上,设P(
上,设P( ,
, ),∴△OPA以OA为底的边上的高是
),∴△OPA以OA为底的边上的高是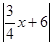 ,当点P在第二象限时,
,当点P在第二象限时,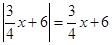 ,∵点A的坐标为(﹣6,0),∴OA=6,∴S=
,∵点A的坐标为(﹣6,0),∴OA=6,∴S=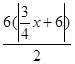 =
=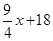 .∵P点在第二象限,∴﹣8<x<0;
.∵P点在第二象限,∴﹣8<x<0;
(3)设点P(m,n)时,其面积S= ,则
,则 ,解得
,解得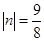 ,则n=
,则n=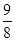 ,n=
,n=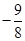 (舍去),当n=
(舍去),当n=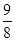 时,
时,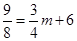 ,则
,则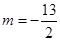 ,故P(
,故P(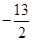 ,
,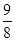 );所以,点P(
);所以,点P(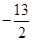 ,
,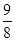 )时,三角形OPA的面积为
)时,三角形OPA的面积为 .
.
考点:一次函数综合题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列四个式子中,是一元一次方程的是( ).
| A.2x-6 | B.x-1=0 | C.2x+y=5 | D.x(x-1)=1 |
下列事件中的必然事件是( )
| A.天气阴了之后下雨 |
| B.小明上学路上看到两车相撞 |
| C.抛掷一枚骰子,朝上的一面点数恰好是5 |
| D.同时抛掷两枚骰子,朝上的两面点数之和小于13 |

 的图象经过点(-l,5),这个函数的表达式为 .
的图象经过点(-l,5),这个函数的表达式为 .
 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: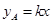 ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额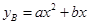 .根据公司信息部的报告,
.根据公司信息部的报告,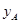 ,
,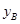 (万元)与投资金额
(万元)与投资金额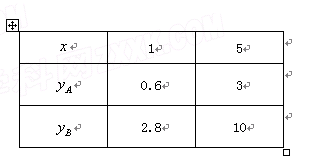
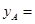 _______________________;
_______________________;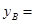 _______________________;
_______________________; (万元),试写出
(万元),试写出