Question

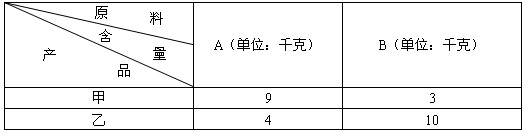
某公司为了开发新产品，用A、B两种原料各360千克、290千克，试制甲、乙两种新型产品共50件，下表是试验每件新产品所需原料的相关数据：

原料 含量 产品	A（单位：千克）	B（单位：千克）
甲	9	3
乙	4	10

（1）设生产甲种产品x件，根据题意列出不等式组，求出x的取值范围；
（2）若甲种产品每件成本为70元，乙种产品每件成本为90元，设两种产品的成本总额为y元，写出成本总额y（元）与甲种产品件数x（件）之间的函数关系式；当甲、乙两种产品各生产多少件时，产品的成本总额最少？并求出最少的成本总额．

Answer 1

分析：（1）关键描述语：用A、B两种原料各360千克、290千克，即所用的A、B两种原料应不大于360千克和290千克，再根据生产两种产品所需各原料的量，列出不等式组即可．
（2）成本总额=甲种产品单价×数量+乙种产品单价×数量，列出关系式进行分析．

解答：解：（1）依题意列不等式组得

9x+4(50-x)≤360① 3x+10(50-x)≤290②

，
由不等式①得x≤32；
由不等式②得x≥30；
∴x的取值范围为30≤x≤32．

（2）y=70x+90（50-x），
化简得y=-20x+4500，
∵-20＜0，
∴y随x的增大而减小．
而30≤x≤32，
∴当x=32，50-x=18时，y_最小值=-20×32+4500=3860（元）．
答：当甲种产品生产32件，乙种18件时，甲、乙两种产品的成本总额最少，最少的成本总额为3860元．

点评：（1）根据原题中已知A、B两种原料的克数即可列出不等式组，求出其公共解集；
（2）根据“成本总额=甲种产品单价×数量+乙种产品单价×数量”列出关系式，根据（1）中所求x的取值范围求出y的最小值即可．