题目内容
如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E, 垂足为F,连接CD,BE
垂足为F,连接CD,BE
(1) 求证:CE=AD
(2) 当点D在AB中点使,四边形BECD是什么特殊四边形?说明理由
(3) 若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由。
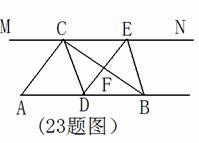
(1)证明:∵DE⊥BC,∠ACB=90°∴AC∥DE,又∵MN∥AB,
∴四边形CADE是平行四边形,∴CE=AD.(5分)
(2)四边形BECD是菱形,理由:D是AB边的中点,所以AD=DB,又AD=CE,所以DB=CE,而DB∥CE,四边形DBEC是平行四边形,
因为ΔACB是直角三角形,D是斜边AB的中点,所以CD=DB,所以四边形BECD是菱形。(4分)
(3)∠A=45°时,四边形BECD是正方形,理由:∵∠ACB=90°又∠A=45°∴CA=CB,点D是AB的中点,∴CD⊥AB,即∠CDB=90°,而四边形BECD是菱形,∴四边形BECD是正方形。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 AB.将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①EF=2BE,②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是
AB.将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①EF=2BE,②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是 C.①③ D.①④
C.①③ D.①④

 ÷(a+1)+
÷(a+1)+ ,其中a=
,其中a=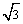 +l.
+l. 的结果是_________.
的结果是_________.
 化为
化为 的形式,结果为( )
的形式,结果为( ) B.
B.
 D.
D.
 的图象先向右平移3 个单位长度,再向下平移2 个单位长度,所得图象的解析式是
的图象先向右平移3 个单位长度,再向下平移2 个单位长度,所得图象的解析式是 则
则 .
. ,则m=__________.
,则m=__________.