��Ŀ����
 ��ͼ��������y=ax2+bx-
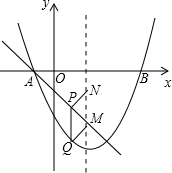
��ͼ��������y=ax2+bx- ����A��-1��0����B��5��0����ֱ��y=-x-1�������ߵĶԳ����ڵ�M����PΪ�߶�AM��һ�㣬����P��PQ��y�ύ�������ڵ�Q������P��PN��QM�������ߵĶԳ����ڵ�N�����P�ĺ�����Ϊm��
����A��-1��0����B��5��0����ֱ��y=-x-1�������ߵĶԳ����ڵ�M����PΪ�߶�AM��һ�㣬����P��PQ��y�ύ�������ڵ�Q������P��PN��QM�������ߵĶԳ����ڵ�N�����P�ĺ�����Ϊm��
��1����a��b��ֵ��
��2���ú�m�Ĵ���ʽ��ʾPQ�ij�����PQ�����ֵ��
��3��ֱ��д��PQ��m���������Сʱm��ȡֵ��Χ��
��4�����ı���PQMN��������ʱ�����m��ֵ��
�⣺��1����A��-1��0����B��5��0������y=ax2+bx- �У���
����
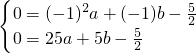 ��
��
��ã�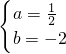 ��
��
��a= ��b=-2��
��b=-2��
��2���ɣ�1����֪a= ��b=-2��
��b=-2��
�������ߵĽ���ʽΪy= x2-2x-
x2-2x- ��
��
�������ߵĶԳ���Ϊx=2��
�ߵ�P�ĺ�����Ϊm��
��P��������m��-m-1������-1��m��2����
��PQ��y�ᣬ
���Q������Ϊm��
��Q���������m�� m2-2m-
m2-2m- ����
����
��PQ=-m-1-�� m2-2m-
m2-2m- ��=-
��=- m2+m+
m2+m+ =-
=- ��m-1��2+2��
��m-1��2+2��
�൱m=1ʱ��PQ�����ֵΪ2��
��3���ɣ�2����֪PQ=-m-1-�� m2-2m-
m2-2m- ��=-
��=- m2+m+
m2+m+ =-
=- ��m-1��2+2��
��m-1��2+2��
��PQ��m���������Сʱm��ȡֵ��Χ��1��m��2��
��4����MN��x��� ����ΪG����G������Ϊ��2��0����
��M��2��-3����
��MG=3��AG=3��
��MG=AG��
���BAM=��AMG=45�㣬
��PQ��y�ᣬMN�ǶԳ��ᣬ
��PQ��MN��
��PN��QM��
���ı���PQMN��ƽ���ı��Σ�
��PN��MN���ı���PQMN�Ǿ��Σ��֡ߡ�BAM=45�㣬
���ı���PQMN�������Σ�
��Q�����������-3���� m2-2m-
m2-2m- =-3��
=-3��
��ã�m1=2- ��m2=2+
��m2=2+ ������������ȥ����
������������ȥ����
��m��ֵ��2- ��
��
��������1���ѵ�A��B��������������߽���ʽ�����㼴�����a��b��ֵ��
��2��������֪��������P������Ϊ��m��-m-1������-1��m��2������ΪPQ��y�ᣬ���Ե�Q������Ϊm������ΪQ���������ϣ�����Q�������Ϊ��m�� m2-2m-
m2-2m- ��������
��������
PQ=-m-1-�� m2-2m-
m2-2m- ��=-
��=- m2+m+
m2+m+ =-
=- ��m-1��2+2�����ú��������ʼ������PQ�����ֵ��
��m-1��2+2�����ú��������ʼ������PQ�����ֵ��
��3�������߶�PQ�ı���ʽת��Ϊ����ʽ����ʽ�����ö��κ����������Խ�ɣ�
��4����MN��x��� ����ΪG����G������Ϊ��2��0��������֤���ı���PQMN��ƽ���ı��Σ���PN��MN���ı���PQMN�Ǿ��Σ�����Ϊ��BAM=45�㣬�����ı���PQMN�������Σ������Q��������Ϊ-3���� m2-2m-
m2-2m- =-3���ⷽ�̼���������������mֵ��
=-3���ⷽ�̼���������������mֵ��
���������⿼���˶��κ������ۺ����ͣ���Ҫ�����˴���ϵ��������κ�������ʽ��ƽ���ı��εĶԱ�ƽ������ȵ����ʣ����κ�������ֵ���⣬���κ����������ԣ��ۺ��Խ�ǿ�����ѶȲ��ѵ�C��������뺯������ʽ���b��c��ֵ�ǽ���Ĺؼ���Ҳ�DZ����ͻ�ƿڣ�
 ����
����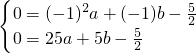 ��
����ã�
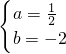 ��
����a=
 ��b=-2��
��b=-2����2���ɣ�1����֪a=
 ��b=-2��
��b=-2���������ߵĽ���ʽΪy=
 x2-2x-
x2-2x- ��
���������ߵĶԳ���Ϊx=2��
�ߵ�P�ĺ�����Ϊm��
��P��������m��-m-1������-1��m��2����
��PQ��y�ᣬ
���Q������Ϊm��
��Q���������m��
 m2-2m-
m2-2m- ����
������PQ=-m-1-��
 m2-2m-
m2-2m- ��=-
��=- m2+m+
m2+m+ =-
=- ��m-1��2+2��
��m-1��2+2���൱m=1ʱ��PQ�����ֵΪ2��
��3���ɣ�2����֪PQ=-m-1-��
 m2-2m-
m2-2m- ��=-
��=- m2+m+
m2+m+ =-
=- ��m-1��2+2��
��m-1��2+2����PQ��m���������Сʱm��ȡֵ��Χ��1��m��2��
��4����MN��x��� ����ΪG����G������Ϊ��2��0����
��M��2��-3����
��MG=3��AG=3��
��MG=AG��
���BAM=��AMG=45�㣬
��PQ��y�ᣬMN�ǶԳ��ᣬ
��PQ��MN��
��PN��QM��
���ı���PQMN��ƽ���ı��Σ�
��PN��MN���ı���PQMN�Ǿ��Σ��֡ߡ�BAM=45�㣬
���ı���PQMN�������Σ�
��Q�����������-3����
 m2-2m-
m2-2m- =-3��
=-3����ã�m1=2-
 ��m2=2+
��m2=2+ ������������ȥ����
������������ȥ������m��ֵ��2-
 ��
����������1���ѵ�A��B��������������߽���ʽ�����㼴�����a��b��ֵ��
��2��������֪��������P������Ϊ��m��-m-1������-1��m��2������ΪPQ��y�ᣬ���Ե�Q������Ϊm������ΪQ���������ϣ�����Q�������Ϊ��m��
 m2-2m-
m2-2m- ��������
��������PQ=-m-1-��
 m2-2m-
m2-2m- ��=-
��=- m2+m+
m2+m+ =-
=- ��m-1��2+2�����ú��������ʼ������PQ�����ֵ��
��m-1��2+2�����ú��������ʼ������PQ�����ֵ����3�������߶�PQ�ı���ʽת��Ϊ����ʽ����ʽ�����ö��κ����������Խ�ɣ�
��4����MN��x��� ����ΪG����G������Ϊ��2��0��������֤���ı���PQMN��ƽ���ı��Σ���PN��MN���ı���PQMN�Ǿ��Σ�����Ϊ��BAM=45�㣬�����ı���PQMN�������Σ������Q��������Ϊ-3����
 m2-2m-
m2-2m- =-3���ⷽ�̼���������������mֵ��
=-3���ⷽ�̼���������������mֵ�����������⿼���˶��κ������ۺ����ͣ���Ҫ�����˴���ϵ��������κ�������ʽ��ƽ���ı��εĶԱ�ƽ������ȵ����ʣ����κ�������ֵ���⣬���κ����������ԣ��ۺ��Խ�ǿ�����ѶȲ��ѵ�C��������뺯������ʽ���b��c��ֵ�ǽ���Ĺؼ���Ҳ�DZ����ͻ�ƿڣ�

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣�
���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣� OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1��
OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��x�ύ�ڵ�A��B����A������Ϊ��-2��0����
��x�ύ�ڵ�A��B����A������Ϊ��-2��0����