题目内容
如图，某施工单位为测得某河段的宽度，测量员先在河对岸边取一点A，再在河这边沿河取两点B、C，在点B处测得点A在北偏东30°方向上，在点C处测得点A在西北方向上，量得BC长为200米，请你求出该河段的宽度（结果保留根号）．
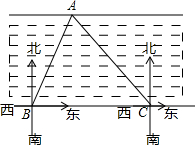
过点A作AD⊥BC于点D．
根据题意，∠ABC=90°-30°=60°，∠ACD=45°，
∴∠CAD=45°，
∴∠ACD=∠CAD，
∴AD=CD，
∴BD=BC-CD=200-AD．
在Rt△ABD中，tan∠ABD=
，
∴AD=BD•tan∠ABD=（200-AD）•tan60°=（200-AD）•
，
∴AD+
AD=200
，
∴AD=
=300-100
．
答：该河段的宽度为（300-100
）米．
根据题意，∠ABC=90°-30°=60°，∠ACD=45°，
∴∠CAD=45°，
∴∠ACD=∠CAD，
∴AD=CD，
∴BD=BC-CD=200-AD．
在Rt△ABD中，tan∠ABD=
| AD |
| BD |
∴AD=BD•tan∠ABD=（200-AD）•tan60°=（200-AD）•
| 3 |
∴AD+
| 3 |
| 3 |
∴AD=
200
| ||
|
| 3 |
答：该河段的宽度为（300-100
| 3 |
练习册系列答案
相关题目
及到的角度用α、β…表示，最后请给出计算MN的高度的式子）．
