题目内容
 在面积为
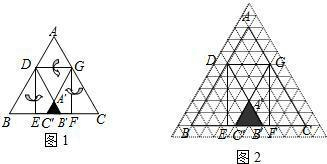
在面积为 的等边△ABC中,AD是BC边上的高,E、F 是AD边上的任意两点,则阴影部分的面积是
的等边△ABC中,AD是BC边上的高,E、F 是AD边上的任意两点,则阴影部分的面积是
- A.

- B.

- C.

- D.4
A
分析:观察图形,证明△BEF与△CEF全等,则阴影部分面积为正三角形面积的一半.
解答:∵△ABC为等边三角形,AD是BC边上的高,
∴AD垂直平分BC,
∴BF=CF BE=CE BD=CD,
又∵EF是公共边,
∴△BEF≌△CEF,
∴S△BEF=S△CEF,
∴阴影部分面积是△ABC面积的一半,
∵S△ABC=4 ,
,
∴阴影部分的面积是2 .
.
故选A.
点评:本题考查了等边三角形的性质,利用对称发现并利用△CEF和△BEF的面积相等是正确解答本题的关键.
分析:观察图形,证明△BEF与△CEF全等,则阴影部分面积为正三角形面积的一半.
解答:∵△ABC为等边三角形,AD是BC边上的高,
∴AD垂直平分BC,
∴BF=CF BE=CE BD=CD,
又∵EF是公共边,
∴△BEF≌△CEF,
∴S△BEF=S△CEF,
∴阴影部分面积是△ABC面积的一半,
∵S△ABC=4
 ,
,∴阴影部分的面积是2
 .
.故选A.
点评:本题考查了等边三角形的性质,利用对称发现并利用△CEF和△BEF的面积相等是正确解答本题的关键.

练习册系列答案
相关题目

 三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果)
三角形A′B′C′的面积,并写出m的取值范围.(直接写出结果) 如图,反比例函数y=
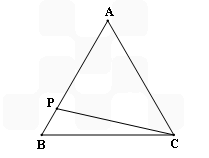
如图,反比例函数y=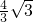 的等边三角形,P是AB边上的动点,设BP=x,△PBC的面积为y.
的等边三角形,P是AB边上的动点,设BP=x,△PBC的面积为y.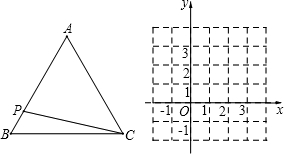
 时,求P点与A点的距离?
时,求P点与A点的距离?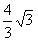 的等边三角形,P是AB边上的动点,设BP=x,△PBC的面积为y。
的等边三角形,P是AB边上的动点,设BP=x,△PBC的面积为y。 时,求P点与A点的距离。
时,求P点与A点的距离。