题目内容
将一根长为16 厘米的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为r和R,面积分别为S1和S2.
厘米的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为r和R,面积分别为S1和S2.
⑴ 求R与r的数量关系式,并写出r的取值范围;
⑵ 记S=S1+S2,求S关于r的函数关系式,并求出S的最小值.
【答案】
(1)0<r<8 (2)S=2π(r-4)2+32π,当r=4厘米时,S有最小值32π平方厘米
【解析】
试题分析:.解:⑴由题意,有2πr+2πR=16π,
则r+R=8,
∵r>0,R>0,∴0<r<8.
即r与R的关系式为r+R=8,r的取值范围是0<r<8厘米;
⑵ ∵r+R=8,∴r=8-R,
∴S=πr2+πR2=πr2+π(8-r)2
=2πr2-16πr+64π
=2π(r-4)2+32π
∴当r=4厘米时,S有最小值32π平方厘米
考点:二次函数的应用
点评:难度中等,考查学生阅读题目和理解题目的能力,列出关系式,利用二次函数的性质解答该题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
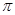 厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为
厘米的细铁丝剪成两段.并把每段铁丝围成圆,设所得两圆半径分别为 和
和 .
.  厘米的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为r和R,面积分别为S1和S2.
厘米的细铁丝剪成两段,并把每段铁丝围成圆,设所得两圆半径分别为r和R,面积分别为S1和S2.