题目内容
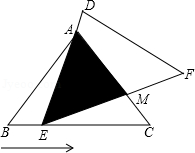
如图，已知正方形ABCD的边长为1，M是AB的中点，则图中阴影部分的面积是
A． | B． |
C． | D． |
D
本试题主要考查了不规则图形的面积计算，本题可以将不易计算图形的面积转化为易计算图形的面积的和差。
因为∵正方形ABCD的面积为1
∴AB=BC=CD=DA=1，AM=
,设MD与AC交于O点，则
∵AM//CD∴△AMO和△COD相似
又∵AM=CD∴S△AMO=S△COD
∵S△DAM=S△CMA（底、高相同）
∴S△DAO=S△CMO
又∵S△DAO+S△AMO=,S△DAO+S△CMO+S△AMO+S△COD=
(梯形面积)
∴S△DAO=,故答案为，选C.
解决该试题的关键是利用S△DAO+S△CMO+S△AMO+S△COD= (梯形面积)得到结论。
因为∵正方形ABCD的面积为1
∴AB=BC=CD=DA=1，AM=
,设MD与AC交于O点，则∵AM//CD∴△AMO和△COD相似
又∵AM=
CD∴S△AMO=S△COD∵S△DAM=S△CMA（底、高相同）
∴S△DAO=S△CMO
又∵S△DAO+S△AMO=
,S△DAO+S△CMO+S△AMO+S△COD= (梯形面积)∴S△DAO=
,故答案为，选C.解决该试题的关键是利用S△DAO+S△CMO+S△AMO+S△COD=
(梯形面积)得到结论。
练习册系列答案
名校课堂系列答案
相关题目
∥
，且
，
，
，求
的长.
，甲数与乙数的比是（ ）
ABCD中，点E在DC上，若EC：AB=2：3，EF=4，则BF= ．
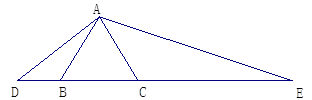
中，
，
，
，
，则
的长为（ ）
