Question

如图，已知AB为⊙O的直径，C为圆上一点，且AC=3，BC=4．CD平分∠ACB，则CD的长为________．

Answer 1

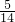分析：作CH⊥AB于H，连结OD、AD、BD，根据圆周角定理得到∠ACB=90°，∠ADB=90°，则根据勾故定理可计算出AB=5，由CD平分∠ACB，得弧AD=弧BD，所以AD=BD，可判断△ABD为等腰直角三角形，所以OD=，利用面积法可计算出CH=，利用勾股定理可计算出AH=，则OH=OA-AH=，由CH∥OD得到△ECH∽△EDO，根据相似的性质得EH：EO=CH：OD=24：25，所以EH=，OE=，在Rt△EHC中利用勾股定理计算出CE=，在Rt△OEH中计算出DE=，所以CD=CE+DE=4．
解答：作CH⊥AB于H，连结OD、AD、BD，如图，
∵AB为⊙O的直径，
∴∠ACB=90°，∠ADB=90°，
∴AB==5，
∵CD平分∠ACB，
∴弧AD=弧BD，
∴AD=BD，
∴△ABD为等腰直角三角形，
∴OD=AB=，
∵AC•BC=CH•AB，
∴CH=，
在Rt△ACH中，AH==，
∴OH=OA-AH=，
∵CH∥OD，
∴△ECH∽△EDO，
∴EH：EO=CH：OD=24：25，
∴EH=×=，OE=，
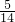在Rt△EHC中，CE==，
在Rt△OEH中，DE==，
∴CD=CE+DE=4．
故答案为4．
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了勾股定理和三角形相似的判定与性质．