题目内容
正方形ABCD中，对角线BD=6
，E是CD上一点，且CE=2
，则∠EBC的度数
- A.15°
- B.30°
- C.45°
- D.60°
B
分析：利用勾股定理计算出正方形的边长，在Rt△ECB中，利用边角关系即三角函数值可求出∠EBC的度数．
解答：
解：∵四边形ABCD是正方形，
∴AB=AD=BC=CD，∠BAD=90°
∴AB2+AC2=BD2，
又∵BD=6，
∴2AB2=72，
∴AB=6，
在Rt△ECB中，tan∠EBC=
=
=
，
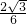∴∠EBC=30°．
故选B．
点评：本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角和特殊角（30°）的三角函数值，属于基础性题目．
分析：利用勾股定理计算出正方形的边长，在Rt△ECB中，利用边角关系即三角函数值可求出∠EBC的度数．
解答：
解：∵四边形ABCD是正方形，∴AB=AD=BC=CD，∠BAD=90°
∴AB2+AC2=BD2，
又∵BD=6
，∴2AB2=72，
∴AB=6，
在Rt△ECB中，tan∠EBC=
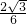==，∴∠EBC=30°．
故选B．
点评：本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角和特殊角（30°）的三角函数值，属于基础性题目．
练习册系列答案
相关题目
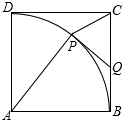△CPQ进行研究．
（2012•徐州）如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC=
（2013•随州）如图，正方形ABCD中，AB=3，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF．下列结论：①点G是BC中点；②FG=FC；③S△FGC=