Question

甲乙两位同学在学完“多边形的内角和”这节内容后，分别动手做了两个有趣的实验，并总结出相关结论。其作法如图所示，阅读后请按要求作题。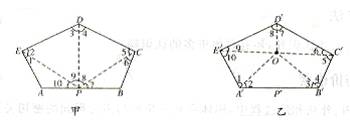

甲：在五边形ABCDE的边AB上取一点P，连结PC、PD、PE，则有

又∵，∴，

即。

乙：在五边形A′B′C′D′E′的内部任取一点O，连结OA′、OB′、OC′、OD′、OE′，则有（ A′O E′）＋（ A′O B′）＋（ B′O C′）＋（ C′O D′）＋（ D′O E′）＝900

又∵ A′O E′+ A′O B′+ B′O C′+ C′O D′+ D′O E′＝360，

∴，

即 E′A′B′+ A′B′C′+ B′C′D′+ C′D′E′+ D′E′A′＝540

（1）填空：甲乙两位同学将　　　　转化为　　　，验证了　　　　。

（2）假如将上述五边形换成n边形，请你分别依据甲、乙两位同学的思路方法验证n边形内角和公式。

Answer 1

答案：
解析：

（1）五边形　　三角形　　五边形内角和为540 （2）按甲同学思路方法：［分为（n-1）个三角形］ 按乙同学思路方法：（分成n个三角形）。

提示：

多边形内角和公式。