题目内容
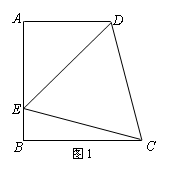
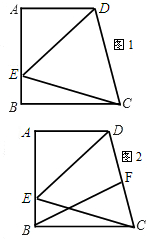
如图1所示,在直角梯形ABCD中,AD∥BC,![]() AB⊥BC,∠DCB=75º,以CD为一边的等边DCE的另一顶点E在腰AB上.
AB⊥BC,∠DCB=75º,以CD为一边的等边DCE的另一顶点E在腰AB上.
(1)求∠AED的度数;
(2)连接AC,试说明:△ABC是等腰三角形;
(3)如图2所示,若F为线段CD上一点,∠FBC=30º.求证: DF =FC;
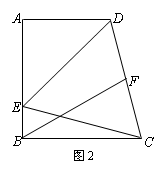 |
(1)∵∠BCD=75º,AD∥BC ∴∠ADC=105º
由等边△DCE可知:∠CDE =60º,故∠ADE =45º
由AB⊥BC,AD∥BC可得:∠DAB=90º , ∴∠AED=45º
(2)方法一:由(1)知:∠AED=45º,∴AD=AE,故点A在线段DE的垂直平分线上.
由△DCE是等边三角形得:CD=CE,故点C也在线段DE的垂直平分线上.
∴AC就是线段DE的垂直平分线,即AC⊥DE
连接AC,∵∠AED =45º,∴∠BAC=45º,又AB⊥BC ∴BA=BC.
∴△ABC为等腰三角形
方法二:过D点作DF⊥BC,交BC于点可证得:△DFC≌△CBE 则DF=BC
从而:AB=CB ∴△ABC为等腰三角形
(3)∵∠FBC=30º,∴∠ABF=60º
连接AF,BF、AD的延长线相交于点G,
∵∠FBC=30º,∠DCB=75º,∴∠BFC=75![]() º,故BC=BF
º,故BC=BF
由(2)知:BA=BC,故BA=BF,∵∠ABF=60º,∴AB=BF=FA,
又∵AD∥BC,AB⊥BC,∴∠FAG=∠G=30º
∴FG =FA= FB
∵∠G=∠FBC=30º,∠DFG=∠CFB,FB=FG
∴△BCF≌△GDF
∴DF=CF

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
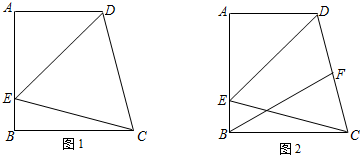
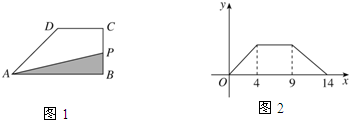
 如图1所示,在直角梯形ABCD中,AD∥BC,∠DCB=75°,AB⊥BC,以CD为一边的等边△DCE的另一顶点E在腰AB上.
如图1所示,在直角梯形ABCD中,AD∥BC,∠DCB=75°,AB⊥BC,以CD为一边的等边△DCE的另一顶点E在腰AB上. .动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为
.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为 
 .动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为(
)
.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为(
) 