��Ŀ����
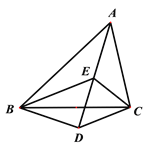
����Ŀ��С����ѧ�������εĽ�ƽ���ߺ���������4����������������������ͼ���ڡ�ABC�У���BAC= 50�㣬��I����ABC����ACBƽ���ߵĽ��㣮

����(1)����գ���BIC��_________�㣮
����(2)������D���������ƽ���ߵĽ��㣬����BDC��_________�㣮
����(3)������E���ڽ���ABC�������ACG��ƽ���ߵĽ��㣬����BEC����BAC��������ϵ��________��
����(4)�������⣨3���������£�����ACB����__________��ʱ��CE��AB��
���𰸡� 115 65 ��BEC![]() ��BAC�����BAC=2��BEC 80
��BAC�����BAC=2��BEC 80
��������������(1)�����ݽ�ƽ���ߵ������Լ��������ڽǺͶ����ó��𰸣�(2)��������������ǵ������Լ��������ڽǺͶ����ó�����֮��Ĺ�ϵ���Ӷ��ó��𰸣�(3)�����������ε��ڽǺͶ����ó��𰸣�(4)������ƽ���ߵ����ʵó���ACE=��A=50����Ȼ����ݽ�ƽ���ߵ����ʵó���ACG=2��ACE=100����Ȼ������������ڽǺͶ����ó��𰸣�
��⣺��1���ߵ�I������B��Cƽ���ߵĽ��㣬
���BIC=180��-����IBC+��ICB��=180��-![]() ����ABC+��ACB��=180��-
����ABC+��ACB��=180��-![]() ��180��-��A��
��180��-��A��
=90+![]() ��BAC=115�㣻
��BAC=115�㣻
��2����BE��BD�ֱ�Ϊ��ABC���ڽǡ����ƽ���ߣ� ���DBI=90�㣬ͬ����DCI=90�㣬
���ı���CDBI�У���BDC=180��-��BIC=90��-![]() ��BAC=65�㣻
��BAC=65�㣻
��3����BEC=![]() ��BAC��
��BAC��
֤�����ڡ�BDE�У���DBI=90�㣬���BEC=90��-��BDC=90��-��90��-![]() ��BAC��=
��BAC��=![]() ��BAC��
��BAC��
��4������ACB����80��ʱ��CE��AB���������£�
��CE��AB�����ACE=��A=50�㣬��CE�ǡ�ACG��ƽ���ߣ����ACG=2��ACE=100�㣬
���ABC=��ACG-��BAC=100��-50��=50�㣬 ���ACB=180��-��BAC-��ABC=80�㣮