��Ŀ����
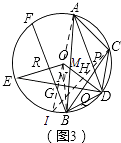
����Ŀ����֪����ABC�ڽ��ڡ�O��D�� ![]() ��һ�㣬OD��BC������ΪH��
��һ�㣬OD��BC������ΪH�� 
��1����ͼ1����Բ��O��AB����ʱ����֤��AC=2OH��
��2����ͼ2����Բ��O�ڡ�ABC�ⲿʱ������AD��CD��AD��BC���ڵ�P����֤����ACD=��APB��
��3���ڣ�2���������£���ͼ3������BD��EΪ��O��һ�㣬����DE��BC�ڵ�Q����AB�ڵ�N������OE��BFΪ��O���ң�BF��OE�ڵ�R��DE�ڵ�G������ACD����ABD=2��BDN��AC=5 ![]() ��BN=3
��BN=3 ![]() ��tan��ABC=
��tan��ABC= ![]() ����BF�ij���
����BF�ij���
���𰸡�
��1���⣺��OD��BC��
���ɴ���������֪����H��BC���е㣬
�ߵ�O��AB���е㣬
��OH�ǡ�ABC����λ�ߣ�
��AC=2OH��
��2���⣺��OD��BC��
���ɴ���������֪�� ![]() ��
��
���BAD=��CAD��
�� ![]() ��
��
���ABC=��ADC��
��180�㩁��BAD����ABC=180�㩁��CAD����ADC��
���ACD=��APB��
��3���⣺����AO�ӳ����ڡ�O�ڵ�I������IC��AB��OD�ཻ�ڵ�M��
�ߡ�ACD����ABD=2��BDN��
���ACD����BDN=��ABD+��BDN��
�ߡ�ABD+��BDN=��AND��
���ACD����BDN=��AND��
�ߡ�ACD+��ABD=180�㣬
���ABD+��BDN=180�㩁��AND��
���AND=180�㩁��AND��
���AND=90�㣬
��tan��ABC= ![]() ��BN=3
��BN=3 ![]() ��
��
��NQ= ![]() ��
��
���ɹ��ɶ�������ã�BQ= ![]() ��
��
�ߡ�BNQ=��QHD=90�㣬
���ABC=��QDH��
��OE=OD��
���OED=��QDH��
�ߡ�ERG=90�㣬
���OED=��GBN��
���GBN=��ABC��
��AB��ED��
��BG=BQ= ![]() ��GN=NQ=
��GN=NQ= ![]() ��
��
��AI�ǡ�Oֱ����
���ACI=90�㣬
��tan��AIC=tan��ABC= ![]() ��
��
�� ![]() =
= ![]() ��
��
��IC=10 ![]() ��
��
���ɹ��ɶ�������ã�AI=25��
����OB��
��QH=x��
��tan��ABC=tan��ODE ![]() ��
��
�� ![]() ��
��
��HD=2x��
��OH=OD��HD= ![]() ��2x��
��2x��
BH=BQ+QH= ![]() +x��
+x��
�ɹ��ɶ����ɵã�OB2=BH2+OH2��
�ࣨ ![]() ��2=��
��2=�� ![]() +x��2+��
+x��2+�� ![]() ��2x��2��
��2x��2��
��ã�x= ![]() ��x=
��x= ![]() ��
��
��QH= ![]() ʱ��
ʱ��
��QD= ![]() QH=
QH= ![]() ��
��
��ND=QD+NQ=6 ![]() ��
��
��MN=3 ![]() ��MD=15
��MD=15
��MD ![]() ��
��
��QH= ![]() ���������⣬��ȥ��
���������⣬��ȥ��
��QH= ![]() ʱ��
ʱ��
��QD= ![]() QH=
QH= ![]()
![]()
��ND=NQ+QD=4 ![]() ��
��
�ɴ�����������ã�ED=10 ![]() ��
��
��GD=GN+ND= ![]()
��EG=ED��GD= ![]()
![]() ��
��
��tan��OED= ![]() ��
��
�� ![]() ��
��
��EG= ![]() RG��
RG��
��RG= ![]() ��
��
��BR=RG+BG=12
���ɴ���������֪��BF=2BR=24��
�����������⿼��Բ���ۺ����⣬�漰Բ�ܽǶ�������λ�ߵ����ʣ�������Ǻ��������ɶ�����֪ʶ���ۺ��Խ�ǿ���������Ҫ�������������ֵ����ݣ���ѧ�����ۺ�����Ҫ��ϸߣ�һ��Ҫע�⽫��ѧ֪ʶ�ᴩ��������1��OD��BC��֪��H��BC���е㣬����λ�ߵ����ʿɵ�AC=2OH����2���ɴ���������֪�� ![]() �����ԡ�BAD=��CAD������Ϊ��ABC=��ADC�����ԡ�ACD=��APB����3���ɡ�ACD����ABD=2��BDN��֪��AND=90�㣬��tan��ABC=
�����ԡ�BAD=��CAD������Ϊ��ABC=��ADC�����ԡ�ACD=��APB����3���ɡ�ACD����ABD=2��BDN��֪��AND=90�㣬��tan��ABC= ![]() ��֪NQ��BQ�ij��ȣ�����BF��OE��OD��BC��֪��GBN=��ABC������BG=BQ������AO���ӳ�����O�ڵ�I������IC������Բ�ܽǶ��������IC��AI�ij��ȣ���QH=x�����ù��ɶ��������QH��HD�ij��ȣ����ô������������ED�ij��ȣ��������tan��OED=
��֪NQ��BQ�ij��ȣ�����BF��OE��OD��BC��֪��GBN=��ABC������BG=BQ������AO���ӳ�����O�ڵ�I������IC������Բ�ܽǶ��������IC��AI�ij��ȣ���QH=x�����ù��ɶ��������QH��HD�ij��ȣ����ô������������ED�ij��ȣ��������tan��OED= ![]() �������RG�ij��ȣ�����ɴ������������BF�ij��ȣ�
�������RG�ij��ȣ�����ɴ������������BF�ij��ȣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�