题目内容
已知点A（x1，y1）、B（x2，y2）都在反比例函数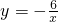
的图象上，若x1x2=-3，则y1y2=________．
-12
分析：根据反比例函数图象上点的坐标特征得到y1=-
，y2=-
，再把它们相乘，然后把x1x2=-3代入计算即可．
解答：根据题意得y1=-，y2=-，
所以y1•y2=-×（-）=
=
=-12．
故答案为-12．
点评：本题考查了反比例函数图象上点的坐标特征：反比例函数y=xk（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
分析：根据反比例函数图象上点的坐标特征得到y1=-
，y2=-，再把它们相乘，然后把x1x2=-3代入计算即可．解答：根据题意得y1=-
，y2=-，所以y1•y2=-
×（-）===-12．故答案为-12．
点评：本题考查了反比例函数图象上点的坐标特征：反比例函数y=xk（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
练习册系列答案
相关题目
已知点A（x1，y1），B（x2，y2），C（x3，y3）是反比例函数y=
在第一象限内的图象上的三个点，且x1＜x2＜x3，则（ ）
| 1 |
| x |
| A、y3＜y2＜y1 |
| B、y2＜y1＜y3 |
| C、y1＜y3＜y2 |
| D、y1＜y2＜y3 |