Question

【题目】已知：在矩形和中，，.

（1）如图1，当点在对角线上，点在边上时，连接，取的中点，连接，，则与的数量关系是_____，_____；

（2）如图2，将图1中的绕点旋转，使点在的延长线上，（1）中的其他条件不变.

①（1）中与的数量关系仍然成立吗？请证明你的结论；

②求的度数.

Answer 1

【答案】（1），；（2），.

【解析】

（1）根据直角三角形斜边上中线性质得ME=MD，根据含有30°的直角三角形性质∠EMC=∠EMF+∠CMF=2（∠MDE+∠MDC）=2∠BDC，由∠DBC=30°，得∠BDC=90°-30°=60°，∠EMC=2∠BDC=2×60°=120°；（2）①分别延长EM，CD交于点G，根据矩形性质证△FEM≌△DGM，得ME=GM，在Rt△GEC中，MC=EG=ME；②如图3，分别延长FE，DB交于点H，证△FEB≌△HEB．得FE=HE．根据EM∥HD，得∠7=∠4=30°，∠7=∠8=30°，∠EMC=180°-∠7-∠8=180°-30°-30°=120°．

（1）如图1，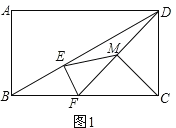
，
∵∠BEF=90°，
∴∠DEF=90°，
∵点M是DF的中点，
∴ME=MD，
∵∠BCD=90°，点M是DF的中点，
∴MC=MD，
∴ME=MC；
∵ME=MD，
∴∠MDE=∠MED，
∴∠EMF=∠MDE+∠MED=2∠MDE，
∵MC=MD，
∴∠MDC=∠MCD，
∴∠CMF=∠MDC+∠MCD=2∠MDC，
∴∠EMC=∠EMF+∠CMF=2（∠MDE+∠MDC）=2∠BDC，
又∵∠DBC=30°，
∴∠BDC=90°-30°=60°，
∴∠EMC=2∠BDC=2×60°=120°．
（2）①ME=MC仍然成立．
证明：如图2，分别延长EM，CD交于点G，
，
∵四边形ABCD是矩形，
∴∠DCB=90°．
∵∠BEF=90°，
∴∠FEB+∠DCB=180°．
∵点E在CB的延长线上，
∴FE∥DC．
∴∠1=∠G．
∵M是DF的中点，
∴FM=DM．
在△FEM和△DGM中，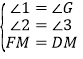
，
∴△FEM≌△DGM，
∴ME=GM，
∴在Rt△GEC中，
MC=EG=ME，
∴ME=MC．
②如图3，分别延长FE，DB交于点H，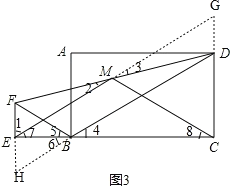
，
∵∠4=∠5，∠4=∠6，
∴∠5=∠6．
∵点E在直线FH上，∠FEB=90°，
∴∠HEB=∠FEB=90°．
在△FEB和△HEB中，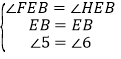
，
∴△FEB≌△HEB．
∴FE=HE．
∵FM=MD，

∴EM是三角形FHD的中位线，
∴EM∥HD，
∴∠7=∠4=30°，
∵ME=MC，
∴∠7=∠8=30°，
∴∠EMC=180°-∠7-∠8=180°-30°-30°=120°．
故答案为：ME=MC，120．