Question

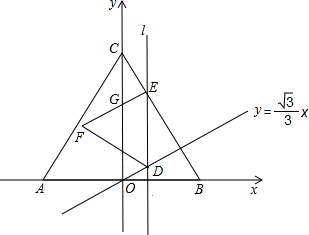（2012•晋江市质检）如图，△ABC是等边三角形，点A坐标为（-8，0）、点B坐标为（8，0），点C在y轴的正半轴上．一条动直线l从y轴出发，以每秒1个单位长度的速度沿x轴向右平移，直线l与直线y=

3

3

x交于点D，与线段BC交于点E．以DE为边向左侧作等边△DEF，EF与y轴的交点为G．当点D与点E重合时，直线l停止运动，设直线l的运动时间为t（秒）．
（1）填空：点C的坐标为

（0，8

3

）

，四边形ODEG的形状一定是

平行四边形

；
（2）试探究：四边形ODEG能不能是菱形？若能，求出相应的t的值；若不能，请说明理由．
（3）当t为何值时，点G恰好落在以DE为直径的⊙M上？并求出此时⊙M的半径．

Answer 1

分析：（1）首先设l与x轴交于点N，由△ABC是等边三角形，点A坐标为（-8，0）、点B坐标为（8，0），易求得OC的长，即可求得点C的坐标，由直线l与直线y=

3

3

x交于点D与△DEF是等边三角形，可证得GE∥OD，又由l∥y轴，可得四边形ODEG是平行四边形；
（2）首先待定系数法求得直线BC的解析式，则可求得点D与E的坐标，即可求得DE的长，又由当OD=DE时，四边形ODEG是菱形，可得方程-

4 3

3

t+8

3

=

2 3

3

t，解此方程即可求得答案；
（3）连接DG，当∠DGE=90°时，点G恰好落在以DE为直径的⊙M上，可得点E是EF的中点，易得当OD=

1

2

DE时，点G恰好落在以DE为直径的⊙M上，即可得方程

2 3

3

t=

1

2

×（-

4 3

3

t+8

3

），解此方程即可求得答案．

解答：解：（1）设l与x轴交于点N，
∵△ABC是等边三角形，点A坐标为（-8，0）、点B坐标为（8，0），
∴OA=OB=8，∠CAB=60°，
∴OC=OA•tan∠CAB=8×

3

=8

3

，
∴点C的坐标为：（0，8

3

），
∵直线l与直线y=

3

3

x交于点D，
∴tan∠DON=

3

3

，
∴∠DON=30°，
∵l⊥x轴，
∴∠DNO=90°，ED∥OC，
∴∠ODN=60°，
∵△DEF是等边三角形，
∴∠FED=60°，
∴∠FED=∠ODN，
∴EF∥OD，
∴四边形ODEG是平行四边形；
故答案为：（0，8

3

），平行四边形；

（2）设直线BC的解析式为：y=kx+b，
∵B（8，0），C（0，8

3

），
∴

8k+b=0 b=8 3

，
解得：

k=- 3 b=8 3

，
∴直线BC的解析式为：y=-

3

x+8

3

，
∴D点坐标为（t，

3

3

t），E（t，-

3

t+8

3

），
则DE=-

3

t+8

3

-

3

3

t=-

4 3

3

t+8

3

，
由（1）知，四边形ODEG是平行四边形，
∴要使四边形ODEG为菱形，则必须有OD=DE成立；
设l与x轴交于点N，
∵OD=2DN=2×

3

3

t=

2 3

3

t，
∴-

4 3

3

t+8

3

=

2 3

3

t，
解得：t=4
∴当t=4秒时，四边形ODEG为菱形；

（3）当t=0时 G．E均与C重合，D与O重合．此时，点G落在以DE为直径的圆M上，
当t≠0时，如图，连接DG，当∠DGE=90°时，点G恰好落在以DE为直径的⊙M上，
∵DF=DE，
∴点G为EF的中点
∴EG=

1

2

EF=

1

2

DE，
由（1）知，四边形ODEG是平行四边形，
∴OD=EG=

1

2

DE，
又由（2）知，DE=-

4 3

3

t+8

3

，OD=

2 3

3

t，
∴

2 3

3

t=

1

2

×（-

4 3

3

t+8

3

），
解得：t=3，
∴当t=3秒时，点G恰好落在以DE为直径的⊙M上，此时⊙M的半径为：

2 3

3

×3=2

3

．

点评：此题考查了待定系数法求一次函数的解析式、等边三角形的性质、平行四边形的判定与性质、菱形的判定以及圆周角定理等知识．此题难度较大，注意掌握符，注意数形结合思想与方程思想的应用．