题目内容
 AB是⊙O的直径,以AB为一边作等边△ABC,交⊙O于点E、F,连接AF,若AB=2,则图中阴影部分的面积为
AB是⊙O的直径,以AB为一边作等边△ABC,交⊙O于点E、F,连接AF,若AB=2,则图中阴影部分的面积为
- A.

- B.

- C.

- D.

D
分析:根据等腰三角形的性质和等弧对等弦得弧AE=弧BF,从而得出阴影部分的面积即为弓形AEF的面积.
解答: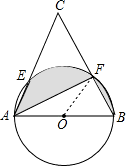 解:连接OF,
解:连接OF,
∵等边△ABC,∴∠ABC=∠BAC=60°,∴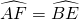 ,∴
,∴ =
=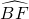 ,AE=BF,∠AOF=120°,
,AE=BF,∠AOF=120°,
∵AB是直径,AB=2,∴AF= ,点O到AF的距离
,点O到AF的距离 ,
,
∴S阴影=S扇形AOF-S△AOF=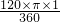 -
- ×
× =
= -
- ,
,
故选D.
点评:本题考查了扇形面积的计算和等边三角形的性质,是基础知识要熟练掌握.
分析:根据等腰三角形的性质和等弧对等弦得弧AE=弧BF,从而得出阴影部分的面积即为弓形AEF的面积.
解答:
 解:连接OF,
解:连接OF,∵等边△ABC,∴∠ABC=∠BAC=60°,∴
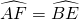 ,∴
,∴ =
=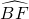 ,AE=BF,∠AOF=120°,
,AE=BF,∠AOF=120°,∵AB是直径,AB=2,∴AF=
 ,点O到AF的距离
,点O到AF的距离 ,
,∴S阴影=S扇形AOF-S△AOF=
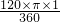 -
- ×
× =
= -
- ,
,故选D.
点评:本题考查了扇形面积的计算和等边三角形的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
 如图,已知AB是⊙O的直径,以B为圆心,BO为半径画弧交⊙O于C,D两点,则∠BCD的度数是( )
如图,已知AB是⊙O的直径,以B为圆心,BO为半径画弧交⊙O于C,D两点,则∠BCD的度数是( )| A、30° | B、50° | C、60° | D、40° |
 如图,AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于点D.
如图,AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于点D. 26、如图,AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于点D,DE⊥OC,垂足为E.
26、如图,AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于点D,DE⊥OC,垂足为E. 16、如图,AB是⊙O的直径,以B为圆心,BO为半径画弧交⊙O于C、D两点,则∠BCD的度数是
16、如图,AB是⊙O的直径,以B为圆心,BO为半径画弧交⊙O于C、D两点,则∠BCD的度数是 23、已知:如图,AB是⊙O的直径,以B为圆心的圆交OB于C,交⊙O于E、F,交AB的延长线于D,连接EC并延长交⊙O于G,
23、已知:如图,AB是⊙O的直径,以B为圆心的圆交OB于C,交⊙O于E、F,交AB的延长线于D,连接EC并延长交⊙O于G,