题目内容
.(8分)如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.试猜想线段BC和EF的数量及位置关系,并证明你的猜想

BC与EF平行且相等, 证明见解析.
【解析】
试题分析:因为AF=CD所以AF+CF=CD+CF即AC=DF又AB=DE,∠A=∠D所以△ABC≌△DEF
由此BC=EF,∠BCA=∠EFD所以BC∥EF,故BC与EF平行且相等
试题解析:∵AF=CD ∴AF+CF=CD+CF 即AC=DF 又∵AB=DE,∠A=∠D∴△ABC≌△DEF ∴BC=EF, ∠BCA=∠EFD ∴BC∥EF ∴BC与EF平行且相等
考点:三角形全等,平行线的判定与性质

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 满足
满足 ,那么
,那么 的值是( )
的值是( ) B.
B. C.
C. D.
D.


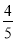 .
.