题目内容

设a、b、c是三个连续的奇数，则


  1. A.
    （abc+4b）能被a3整除
  2. B.
    （abc+4b）能被b3整除
  3. C.
    （abc+4b）能被c3整除
  4. D.
    （abc+4b）能被abc整除
B
分析：首先根据连续奇数的特点，用含b的代数式表示a、c，然后化简abc+4b，即可得出结果．
解答：∵a、b、c是三个连续的奇数，
∴a+2=b=c-2，
∴a=b-2，c=b+2，
∴abc+4b=（b-2）b（b+2）+4b=b3，
∴（abc+4b）能被b3整除．
故选B．
点评：本题考查了连续奇数的定义及代数式的化简，注意利用连续奇数的差是2．
练习册系列答案
相关题目
已知抛物线y=-
23
（x+2）2+k与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，C点在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2-10x+16=0的两个根．
（1）求A、B、C三点的坐标；
（2）在平面直角坐标系内画出抛物线的大致图象并标明顶点坐标；
（3）连AC、BC，若点E是线段AB上的一个动点（与A、B不重合），过E作EF∥AC交BC于F，连CE，设AE=m，△CEF的面积为S，求S与m的函数关系式，并写出自变量m的取值范围；
（4）在（3）的基础上说明S是否存在最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．
（2010•河北区模拟）若二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个不同的交点A（1，0）、B（-3，0），与y轴的负半轴交于点C，且S△ABC=6．
（Ⅰ）求该二次函数的解析式和顶点P的坐标；
（Ⅱ）经过A、B、P三点画⊙O′，求⊙O′的面积；
（Ⅲ）设抛物线上有一动点M（a，b），连AM，BM，试判断△ABM能否是直角三角形？若能，求出M点的坐标；若不能，请说明理由．
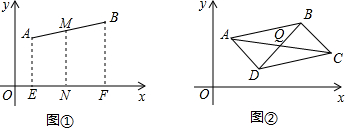让我们一起来探索平面直角坐标系中平行四边形的顶点的坐标之间的关系．
第一步：数轴上两点连线的中点表示的数．自己画一个数轴，如果点A、B分别表示-2、4，则线段AB的中点M表示的数是
1
1
． 再试几个，我们发现：数轴上连接两点的线段的中点所表示的数是这两点所表示数的平均数．
第二步；平面直角坐标系中两点连线的中点的坐标（如图①）为便于探索，我们在第一象限内取两点A（x1，y1），B（x2，y2），取线段AB的中点M，分别作A、B到x轴的垂线段AE、BF，取EF的中点N，则MN是梯形AEFB的中位线，故MN⊥x轴，利用第一步的结论及梯形中位线的性质，我们可以得到点M的坐标是（
x1+x2
2
x1+x2
2
，
y1+y2
2
y1+y2
2
 ）（用x1，y1，x2，y2表示），AEFB是矩形时也可以．我们的结论是：平面直角坐标系中连接两点的线段的中点的横（纵）坐标等于这两点的横（纵）坐标的平均数．
第三步：平面直角坐标系中平行四边形的顶点坐标之间的关系（如图②）在平面直角坐标系中画一个平行四边形ABCD，设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），则其对角线交点Q的坐标可以表示为Q（
x1+x3
2
x1+x3
2
，
y1+y3
2
y1+y3
2
），也可以表示为Q（
x2+x4
2
x2+x4
2
，
y2+y4
2
y2+y4
2
 ），经过比较，我们可以分别得出关于x1，x2，x3，x4及，y1，y2，y3，y4的两个等式是
x1+x3=x2+x4
x1+x3=x2+x4
和
y1+y3=y2+y4
y1+y3=y2+y4
． 我们的结论是：平面直角坐标系中平行四边形的对角顶点的横（纵）坐标的
和相等
和相等
．
以下所提供的材料有三组不同角度的问题，第一组为必答题，第二三组你可以自主选择其中一组探究并作答。

材料一：“丞相之印章”封泥

材料二：周亚夫；汉文、景之世名将。周勃次子，因兄胜之杀人被处死，故得嗣爵，封为条侯。文帝后元六年（前158）,匈奴大举侵扰上郡、云中，京城长安告警。周亚夫以河内太守被任为将军，驻屯细柳。因治军谨严有方，不久迁中尉，负责京城治安。汉景帝刘启即位后，任亚夫为车骑将军三年（前154）吴楚七国发动叛乱（见吴楚七国之乱），周亚夫以太尉率军平叛。他会兵荥阳，固守昌邑,待机以轻骑断绝吴军粮道。最后以精兵出击,不到三个月,就平定了叛乱。五年后，周亚夫迁为丞相,很受景帝器重。不久,因不同意废栗太子,又在王皇后兄王信和匈奴降王徐卢五人封侯等政事上与景帝旨意相左，加以梁孝王的挑拨和诬陷,受到景帝猜忌, 中元三年(前147)被免除丞相职务。景帝后元元年（前143）,周亚夫子私买工官尚方甲盾五百具，备作其父葬器，被人告发，事连周亚夫。廷尉召亚夫对质，并逼其供认谋反。周亚夫不服，绝食五日，呕血而死。
材料三：唐太宗说：“以天下之广、四海之众，千端万绪须合变通，皆委百司商量、宰相筹划，于事稳便，方可奏行。岂得以一日万机，独断一人之虑也。且日断十事，五条不中，中者信善，其如不中者何？以日继月，乃至累年，乖谬既多，不亡何待？”
——《贞观政要》
材料四：明太祖说：“自秦始置丞相，不旋踵而亡。汉唐宋因之，虽有贤相，然其间所有者，多有小人，专权乱政。今我朝罢丞相，设五府、六部分理天下庶务，彼此颉颃不敢相压。事皆朝廷总之，所以稳当。”
——《明史纪事本末》
请回答：
第一组：①依照秦朝官制，丞相一职的主要职责是什么？
②依据材料一，周亚夫被免于丞相职务的原因是什么？ 其根本原因又是什么？
③周亚夫曾经做过太尉，后来被廷尉逼供而死，太尉是什么官职？廷尉又是什么官职？
④周亚夫被封为条侯和后来被封为车骑将军，被封的原因有何不同？
⑤前后两种不同的任职原因说明古代中国的选官制度的什么发展趋势？
第二组：⑥唐太宗认为“稳便”的途径是什么？
⑦唐太宗与明太祖在制度设置上看法有何不同？
第三组：⑧明太祖认为“稳当”的方法是什么？
⑨据材料，你认为唐太宗与明太祖的看法从根本上说是否矛盾？
以下所提供的材料有三组不同角度的问题，第一组为必答题，第二三组你可以自主选择其中一组探究并作答。

材料一：“丞相之印章”封泥

材料二：周亚夫；汉文、景之世名将。周勃次子，因兄胜之杀人被处死，故得嗣爵，封为条侯。文帝后元六年（前158）,匈奴大举侵扰上郡、云中，京城长安告警。周亚夫以河内太守被任为将军，驻屯细柳。因治军谨严有方，不久迁中尉，负责京城治安。汉景帝刘启即位后，任亚夫为车骑将军三年（前154）吴楚七国发动叛乱（见吴楚七国之乱），周亚夫以太尉率军平叛。他会兵荥阳，固守昌邑,待机以轻骑断绝吴军粮道。最后以精兵出击,不到三个月,就平定了叛乱。五年后，周亚夫迁为丞相,很受景帝器重。不久,因不同意废栗太子,又在王皇后兄王信和匈奴降王徐卢五人封侯等政事上与景帝旨意相左，加以梁孝王的挑拨和诬陷,受到景帝猜忌, 中元三年(前147)被免除丞相职务。景帝后元元年（前143）,周亚夫子私买工官尚方甲盾五百具，备作其父葬器，被人告发，事连周亚夫。廷尉召亚夫对质，并逼其供认谋反。周亚夫不服，绝食五日，呕血而死。
材料三：唐太宗说：“以天下之广、四海之众，千端万绪须合变通，皆委百司商量、宰相筹划，于事稳便，方可奏行。岂得以一日万机，独断一人之虑也。且日断十事，五条不中，中者信善，其如不中者何？以日继月，乃至累年，乖谬既多，不亡何待？”
——《贞观政要》
材料四：明太祖说：“自秦始置丞相，不旋踵而亡。汉唐宋因之，虽有贤相，然其间所有者，多有小人，专权乱政。今我朝罢丞相，设五府、六部分理天下庶务，彼此颉颃不敢相压。事皆朝廷总之，所以稳当。”
——《明史纪事本末》
请回答：
第一组：①依照秦朝官制，丞相一职的主要职责是什么？
②依据材料一，周亚夫被免于丞相职务的原因是什么？ 其根本原因又是什么？
③周亚夫曾经做过太尉，后来被廷尉逼供而死，太尉是什么官职？廷尉又是什么官职？
④周亚夫被封为条侯和后来被封为车骑将军，被封的原因有何不同？
⑤前后两种不同的任职原因说明古代中国的选官制度的什么发展趋势？
第二组：⑥唐太宗认为“稳便”的途径是什么？
⑦唐太宗与明太祖在制度设置上看法有何不同？
第三组：⑧明太祖认为“稳当”的方法是什么？
⑨据材料，你认为唐太宗与明太祖的看法从根本上说是否矛盾？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网