Question

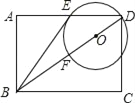
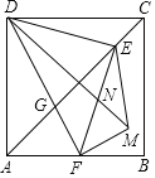
【题目】如图，正方形ABCD中，AD＝6，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若AF=2，则的面积为__．

Answer 1

【答案】

【解析】

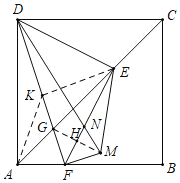
如图，取DF的中点K，连接AK，EK．连接GM交EF于H．首先证明△DEF是等腰直角三角形求出DE，EF，解直角三角形求出EN，MH即可解决问题．

解：如图，取DF的中点K，连接AK，EK．连接GM交EF于H．

∵四边形ACD是正方形，

∴AD=AB=6，∠DAB=90°，AB∥CD，∠DAC=∠CAB=45°，

∵DE⊥EF，

∴∠DEF=∠DAF=90°，

∵DK=KF，

∴KA=KD=KF=KE，

∴A，F，E，D四点共圆，

∴∠DFE=∠DAE=45°，

∴∠EDF=∠EFD=45°，

∴DE=EF，

∵AF=2，AD=6，

∴DF=，

∴DE=EF=，

∵AF∥CD，

∴，

∴FG=FM=，

∴GM=FM=，

∴FH=GH=HM=，

∵EF⊥GM，

∴GH=HM=，

∴EH=EF-FH=，

∵MH∥DE，

∴，

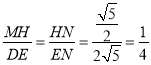∴EN=，
∴S△ENM=ENMH=．

故答案为：．