题目内容
 按题意填空:
按题意填空:
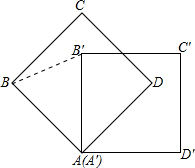
如图,正方形A′B′C′D′是正方形ABCD按顺时针方向旋转45°而成的.
(1)若AB=4,则S□ABCD=______;
(2)∠BAB′=______,∠B′AD=______;
(3)若连接BB′,则∠B′BA=______.
 解:(1)S□ABCD=AB2=42=16.
解:(1)S□ABCD=AB2=42=16.故答案是:16;
(2)∵如图,正方形A′B′C′D′是正方形ABCD按顺时针方向旋转45°而成的,点A与点A′对应,且点A与点A′重合,点B与点B′对应,
∴点A是旋转中心,∠BAB′是旋转角,
∴∠BAB′=45°.
又∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠B′AD=∠BAD-∠BAB′=90°-45°=45°.
故答案是:45°,45°;
(3)如图,连接BB′.
∵根据旋转的性质知,AB=AB′,
∴∠B′BA=∠BB′A.
由(2)知,∠BAB′=45°,
∴∠B′BA=
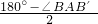 =
= =67.5°.
=67.5°.故答案是:67.5°.
分析:(1)根据正方形的面积公式求解;
(2)根据旋转的性质找到旋转角是∠BAB′=45°;然后由正方形的性质和图形中角与角间的和差关系求得∠B′AD=∠BAD-∠BAB′=90°-45°=45°;
(3)由旋转的性质知AB=AB′.所以根据“等边对等角”、三角形内角和定理来求∠B′BA的度数.
点评:本题考查了旋转的性质,正方形的性质.解答(3)题时,推知△ABB′的等腰三角形是求∠B′BA的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
在数学中玩,在玩中学数学
1:某车间2005年的产值为a万元,以后每年产值均比上一年增长x%.
(1)用代数式表示2006年和2007年的产值;
(2)当a=100,x=10,求2007年的产值.
2:如图,点C在线段AB上,AC=8cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?

3:第一行的图形绕虚线转一周,能形成第二行的某个几何体,按要求填空.
图1旋转形成 ,图2旋转形成 ,图3旋转形成 ,图4旋转形成 ,图5旋转形成 ,图6旋转形成 .
4:如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
(2)原正方形能否被分割成2004个三角形?若能,求此时正方形ABCD内部有多少个点;若不能,请说明理由.
1:某车间2005年的产值为a万元,以后每年产值均比上一年增长x%.
(1)用代数式表示2006年和2007年的产值;
(2)当a=100,x=10,求2007年的产值.
2:如图,点C在线段AB上,AC=8cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.你能用一句简洁的话描述你发现的结论吗?

3:第一行的图形绕虚线转一周,能形成第二行的某个几何体,按要求填空.

图1旋转形成
4:如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
| 分割成的三角形的个数 | 4 | 6 | … |



 按题意填空:
按题意填空: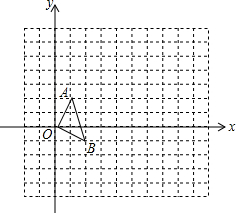 【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
【问题】在正方形网格中,如图(一),△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).